Геометричний метод
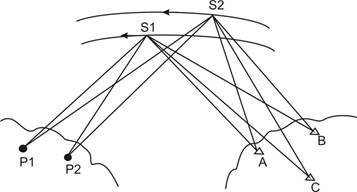
Геометричний метод ґрунтується на синхронному фотографуванні ШСЗ на фоні зоряного неба мінімально з двох пунктів поверхні Землі. Такі спостереження дають можливість визначати напрям вектора, який з’єднує ці пункти. Множина таких векторів утворює векторну просторову мережу, яка називається космічною тріангуляцією. Таким методом можна будувати мережі зі сторонами порядку 1,5 – 2000 км, а також зв’язати материки та острова в єдиній системі координат.
Рис. 1.1 Схема застосування геометричного методу
Перевагою геометричного методу є те, що він виключає знання теорії рухів супутника, а також фактори, які складно враховуються (коливання орбіти, аномалія гравітації, опір атмосфери). Недоліки геометричного методу: - при цьому методі визначаються лише відносні положення нових пунктів в системі вихідних координат; - неможливо прив’язати мережу космічної тріангуляції до центру мас Землі. В основі геометричного методу лежить фундаментальне рівняння супутникової геодезії. По суті воно пов’язує три вектори r, r', R (рис. 1.2)
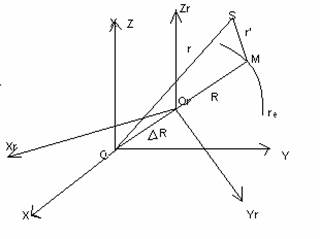
Рис. 1.2 Виведення фундаментального рівняння супутникової геодезії
На рисунку: OXYZ – геоцентрична система координат, початок якої в центрі мас землі О; OrXrYrZr – референцна система координат; М – точка, яка знаходиться на поверхні референц–еліпсоїда; S – супутник; R – радіус–вектор пункту М, який віднесений до центра Or – референц–еліпсоїда; r – геоцентричний радіус–вектор супутника; r' - топоцентричний радіус–вектор супутника. З рисунка очевидно, що фундаментальне рівняння має
вигляд:
Звідси:
r=r'+R+ΔR. (1.1)
R=r- r'- ΔR, (1.2) r'= r- R –ΔR. (1.3) Нехай маємо дві точки на земній поверхні – М1 і М2. З рівняння (1.3) впливає: r'1= r- R1–ΔR (1.4) r'2= r- R2–ΔR. Віднявши ці рівняння одержимо: r'2- r'1= R1- R2. (1.5). Якщо координати точки М1 відомі, то рівняння (1.5) дає змогу визначити координати точки М2 відносно координат точки М1. На сучасному етапі розвитку комп’ютерної техніки складність обчислення руху супутників вже перестала бути перевагою даного методу. На даний час найбільше використовується динамічний метод супутникової геодезії. 1.4.2. Динамічний метод Найбільш загальним методом для вирішення задач супутникової геодезії є динамічний, який ґрунтується на вивченні еволюції орбіти ШСЗ в часі. Тобто, необхідно знати модель руху супутника.
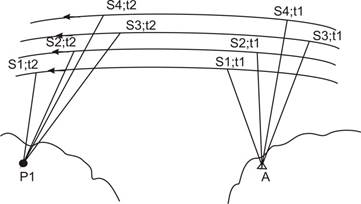
Рис. 1.3 Схема динамічного методу
Математична модель руху супутника в інерціальній системі прямокутних координат записується в системі трьох нелінійних диференціальних рівнянь другого порядку, в правій частині яких знаходяться члени, які враховують прискорення всіх сил, що впливають на рух. Таким чином, точність результатів, одержаних за допомогою динамічного методу, залежать від точності врахування збурюючих прискорень, які викликані всіма силами, що діють на супутники. До них відносяться: сила тяжіння, опір атмосфери, притягання супутника Місяцем, Сонцем, планетами, тиском сонячного випромінювання тощо. В загальному за допомогою динамічного методу можна сумісно визначати координати земних пунктів, елементи орбіт супутників та уточнення збурюючих параметрів сил. Такі задачі вирішуються методами послідовних наближень. Перевагою методу є можливість одержання положення пунктів в єдиній для всієї планети системі координат з початком в центрі мас Землі та визначення гравітаційного поля Землі в цій же системі координат. Вдосконалення динамічного методу дасть можливість розв’язувати головні задачі геодезії та геодинаміки. Фундаментальне рівняння для динамічного методу має складніший вигляд. В даному випадку геоцентричний радіус r є складною функцією від елементів орбіти, параметрів гравітаційного поля і часу: r = r(Еі,ψk,t). (1.6) Тоді
r' = r(Еі,ψk,t)-R, (1.7) при цьому будемо вважати, що t=const. (1.8) Для визначення рівняння і поправок у вимірюванні топоцентричної віддалі необхідно перейти до лінійного перетворення рівняння (1.7):
r r Dy r DR (r' - r'
) V, (1.9) r Es s r y k R 0 вим r де: r'вим. – виміряний топоцентричний радіус, ' Es, k, R - поправки до величин, r 0 - наближене значення топоцентричного радіус – вектора до супутника, Vr– імовірна поправка до виміряної величини. Коли елементи орбіти і параметри гравітації відомі, то рівняння (1.9) набуває спрощеного вигляду:
(1.10) R 0 вим r і тоді, маючи певну кількість вимірювань r'вим., можна знайти поправки до ΔR і достовірне значення виміряної величини.
|


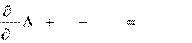 r R (r' r') V
r R (r' r') V


