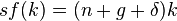Доход расходуется на потребление и инвестиции, соответственно тождество дохода 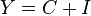 , или в удельном выражении на единицу труда с постоянной эффективностью -
, или в удельном выражении на единицу труда с постоянной эффективностью -  . Инвестиции равны сбережениям
. Инвестиции равны сбережениям 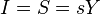 или на единицу трудовых ресурсов
или на единицу трудовых ресурсов  , где
, где  - норма сбережений. Предполагается постоянный темп износа капитала
- норма сбережений. Предполагается постоянный темп износа капитала  и соответственно модель динамики капитала имеет вид:
и соответственно модель динамики капитала имеет вид:
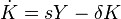
или в удельном представлении:
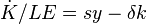
С другой стороны, учитывая, что по определению  имеем:
имеем:
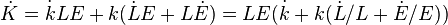
Следовательно, можно записать окончательно базовое дифференциальное уравнение модели Солоу:
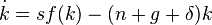
где  - темп роста населения (работников);
- темп роста населения (работников);  - темп технического прогресса;
- темп технического прогресса;
Таким образом, если инвестиции  меньше необходимого уровня
меньше необходимого уровня  , учитывающего рост населения и износ капитала и технический прогресс, то капиталовооруженность труда с постоянной эффективностью падает и наоборот. Равновесный уровень определяется исходя из условия стабильности
, учитывающего рост населения и износ капитала и технический прогресс, то капиталовооруженность труда с постоянной эффективностью падает и наоборот. Равновесный уровень определяется исходя из условия стабильности  , то есть
, то есть  . Соответственно условие стационарности следующее (совпадение фактических и необходимых инвестиций):
. Соответственно условие стационарности следующее (совпадение фактических и необходимых инвестиций):
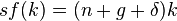
В модели Солоу в стационарном состоянии темп роста производительности труда равен темпу технического прогресса, а темп экономического роста - сумме темпа технического прогресса и темпа роста населения.
При росте нормы сбережений инвестиции начинают превышать необходимый уровень и  начинает расти до достижения равновесия при более высоком уровне
начинает расти до достижения равновесия при более высоком уровне  . В процессе перехода к новому стационарному состоянию темп роста производительности труда будет опережать темп технического прогресса и при достижении нового равновесия они приравняются.
. В процессе перехода к новому стационарному состоянию темп роста производительности труда будет опережать темп технического прогресса и при достижении нового равновесия они приравняются.

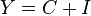 , или в удельном выражении на единицу труда с постоянной эффективностью -
, или в удельном выражении на единицу труда с постоянной эффективностью -  . Инвестиции равны сбережениям
. Инвестиции равны сбережениям 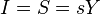 или на единицу трудовых ресурсов
или на единицу трудовых ресурсов  , где
, где  - норма сбережений. Предполагается постоянный темп износа капитала
- норма сбережений. Предполагается постоянный темп износа капитала  и соответственно модель динамики капитала имеет вид:
и соответственно модель динамики капитала имеет вид: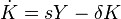
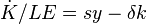
 имеем:
имеем: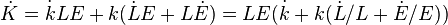
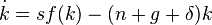
 - темп роста населения (работников);
- темп роста населения (работников);  - темп технического прогресса;
- темп технического прогресса; меньше необходимого уровня
меньше необходимого уровня  , учитывающего рост населения и износ капитала и технический прогресс, то капиталовооруженность труда с постоянной эффективностью падает и наоборот. Равновесный уровень определяется исходя из условия стабильности
, учитывающего рост населения и износ капитала и технический прогресс, то капиталовооруженность труда с постоянной эффективностью падает и наоборот. Равновесный уровень определяется исходя из условия стабильности  , то есть
, то есть  . Соответственно условие стационарности следующее (совпадение фактических и необходимых инвестиций):
. Соответственно условие стационарности следующее (совпадение фактических и необходимых инвестиций):