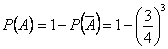Примеры. Задача 1. По мишени стреляют три стрелка
Задача 1. По мишени стреляют три стрелка. Вероятности попадания соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что попадут все три. Решение: Пусть событие А- попал 1-й, В- 2-й и С-3-й. Эти события независимые, тогда применяя соответствующую теорему, получим, что вероятность совместного появления всех трех событий равна: Р(АВС)=Р(А)Р(В)Р(С)=0,7·0,8·0,9=0,504. Задача 2. В урне находятся 3 белых, 2 черных и 4 синих шара. Какова вероятность того, что первым будет вынут белый шар, вторым- синий, третьим- черный. Шары не возвращаются. Решение: Пусть события: А- вынут белый шар, В- вынут синий, С- черный. Вероятность, что первым вынут белый равна
Событие В происходит после события А, при этом условия меняются- общее количество шаров уменьшилось и стало равно 8, поэтому события А и В зависимые и речь идет об условной вероятности события В: РА(В)=4/8=1/2. Событие С происходит после событий А и В, поэтому вероятность его тоже условная РАВ(С)=2/7. Вероятность же их совместного появления:
Задача 3. В группе 20 студентов. Из них двое курят, 12 – в очках, 6 – курят и носят очки. Найти вероятность того, что студент курит, если он носит очки. Решение. Пусть событие Тогда Заметим, что условная и безусловная вероятности события
События называются независимыми, если появление одного из них не влияет на вероятность появления другого:
Если события независимые, то теорема умножения вероятностей принимает вид: В рассмотренном примере события Задача 4. Бросают три монетки и игральную кость. Событие Задача 5. Три грани треугольной пирамиды окрашены соответственно в белый, зеленый, желтый цвета. На последней грани присутствуют все три цвета. Случайным образом выбирают грань. Найти вероятности событий: Решение. Желтый цвет имеется на двух гранях из четырех, т.о. Т.е. все события попарно независимы. Однако события не являются независимыми в совокупности: Задача 6. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая карта. Решение. Пусть событие Задача 7 Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Найти вероятность попадания в мишень при одном выстреле.
|

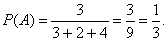
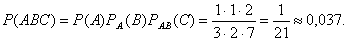
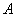 - студент курит;
- студент курит; 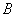 - студент носит очки.
- студент носит очки.
 .
.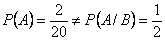 .
.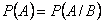 .
.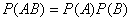 - критерий независимости событий.
- критерий независимости событий.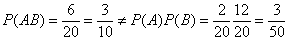 .
.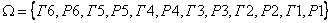 . Тогда
. Тогда 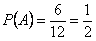 ,
, 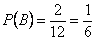 ,
, 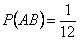 . Таким образом,
. Таким образом, 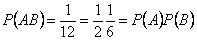 , т.е. события
, т.е. события 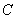 =«на грани есть зеленый цвет»;
=«на грани есть зеленый цвет»;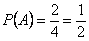 ; аналогично:
; аналогично: 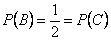 . Вероятность того, что на выпавшей грани есть два цвета -
. Вероятность того, что на выпавшей грани есть два цвета - 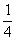 , т.е.
, т.е. 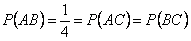 . Таким образом,
. Таким образом,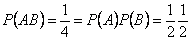
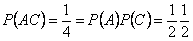
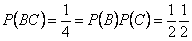 ,
,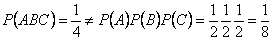
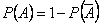 . Событие
. Событие 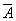 означает, что все четыре карты не бубновой масти. Вероятность того, что случайно взятая из колоды карта не бубновая - и
означает, что все четыре карты не бубновой масти. Вероятность того, что случайно взятая из колоды карта не бубновая - и 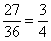 , тогда
, тогда 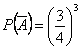 ,
,