БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если
Функция f(x) =(x -1)2 является бесконечно малой при x →1, так как Функция f(x) = tg x – бесконечно малая при x →0. f(x) = ln (1+ x)– бесконечно малая при x →0. f(x) = 1/ x – бесконечно малая при x →∞. Установим следующее важное соотношение: Теорема. Если функция y=f(x) представима при x→a в виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то Обратно, если Доказательство. Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<;ε. Тогда |f(x) – b|<; ε. А это и значит, что Если Рассмотрим основные свойства бесконечно малых функций. Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая. Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где Итак, зафиксируем произвольное число ε >;0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1 >;0, что при |x – a|<;δ1 имеем |α(x)|<; ε / 2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2 >;0, что при |x – a|<;δ2 имеем | β(x)|<; ε / 2. Возьмем δ=min{ δ1, δ2 }. Тогда в окрестности точки a радиуса δ;будет выполняться каждое из неравенств |α(x)|<; ε / 2 и | β(x)|<; ε / 2. Следовательно, в этой окрестности будет |f(x)|=| α(x)+β(x) | ≤ |α(x)| + | β(x)| <; ε /2 + ε /2= ε, т.е. |f(x)|<;ε, что и требовалось доказать. Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞;) есть бесконечно малая функция. Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε >;0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|<; ε /M. Тогда в меньшей из этих окрестностей имеем | αf|<; ε /M = ε. А это и значит, что af – бесконечно малая. Для случая x→∞; доказательство проводится аналогично. Из доказанной теоремы вытекают: Следствие 1. Если Следствие 2. Если Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция. Доказательство. Пусть
СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1 /f(x) является бесконечно малой при x→a. Доказательство. Возьмем произвольное число ε >0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x, для которых |x – a|<δ;, выполняется неравенство Примеры. Ясно, что при x→+∞ функция y=x2+ 1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция
Можно доказать и обратную теорему. Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y= 1 /f(x) является бесконечно большой функцией.
Примеры.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A ≠ 0
|

 или
или  , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.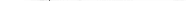 Примеры.
Примеры. (см. рис.).
(см. рис.). .
. и
и  . Нам нужно доказать, что при произвольном как угодно малом ε >;0 найдется δ>;0, такое, что для x, удовлетворяющих неравенству |x – a|<δ;, выполняется |f(x)|<; ε.
. Нам нужно доказать, что при произвольном как угодно малом ε >;0 найдется δ>;0, такое, что для x, удовлетворяющих неравенству |x – a|<δ;, выполняется |f(x)|<; ε. .
.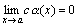 .
. . Тогда 1 /f(x) есть ограниченная функция. Поэтому дробь
. Тогда 1 /f(x) есть ограниченная функция. Поэтому дробь  есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.
есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.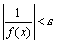 , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a, то найдется δ>0 такое, что как только |x – a|<δ;, так | f(x)|>;1 / ε. Но тогда для тех же x
, а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a, то найдется δ>0 такое, что как только |x – a|<δ;, так | f(x)|>;1 / ε. Но тогда для тех же x  – бесконечно малая при x→+∞;, т.е.
– бесконечно малая при x→+∞;, т.е. 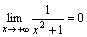 .
. .
. .
. .
. , так как функции
, так как функции  и
и  - бесконечно малые при x→+∞;, то
- бесконечно малые при x→+∞;, то  , как сумма бесконечно малых функций есть функция бесконечно малая. Функция же
, как сумма бесконечно малых функций есть функция бесконечно малая. Функция же  является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство.
является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство. .
.


