Графический способ
Числовые функции можно также задавать с помощью графика. Пусть Рассмотрим некоторое (n+1)-мерное линейное пространство над полем вещественных чисел (так как функция вещественная). Выберем в этом пространстве любой базис ( Если в качестве линейного пространства взять евклидово пространство свободных геометрических векторов (направленных отрезков), а число аргументов функции f не превосходит 2, указанное множество точек можно изобразить наглядно в виде чертежа (графика). Если сверх того исходный базис взять ортонормированным, получим "школьное" определение графика функции. Для функций 3 аргументов и более такое представление не применимо ввиду отсутствия у человека геометрической интуиции многомерных пространств. Однако, и для таких функций можно придумать наглядное полугеометрическое представление (например каждому значению четвертой координаты точки сопоставить некоторый цвет на графике)
Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k x,
где k - постоянная величина (коэффициент пропорциональности). График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x, где k - постоянная величина.
Основные характеристики и свойства гиперболы: - область определения функции: x - функция монотонная (убывающая) при x < 0и при x > 0, но не монотонная в целом из-за точки разрыва x = 0); - функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая; - нулей функция не имеет.
Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a
Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x 2 и дискриминанта D: D = b 2 – 4 ac. Эти свойства следуют из анализа корней квадратного уравнения (см. соответствующий раздел в главе «Алгебра»). Все возможные различные случаи для квадратной параболы показаны на рис.12.
- область определения функции: ; значений: … (ответьте, пожалуйста, на этот вопрос сами!); - функция в целом не монотонна, но справа или слева от вершины ведёт себя, как монотонная; - функция неограниченная, всюду непрерывная, чётная при b = c = 0, и непериодическая; - при D < 0 не имеет нулей.
- область определения функции: ; область значений: y > 0; - функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - нулей функция не имеет.
Основные характеристики и свойства логарифмической функции: - область определения функции: x > 0,а область значений: ; (т.e. y - это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - у функции есть один ноль: x = 1.
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция y = sin x представляется графиком (рис.19). Эта кривая называется синусоидой.
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на
Из этих графиков очевидны характеристики и свойства этих функций: - область определения: ; - эти функции периодические: их период 2 - функции ограниченные (| y | имеющие так называемые интервалы монотонности, внутри которых они ведут себя, как монотонные функции (см. графики рис.19 и рис.20); - функции имеют бесчисленное множество нулей (подробнее см. раздел «Тригонометрические уравнения»).
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
Из графиков видно, что эти функции: периодические (их период неограниченные, в целом не монотонные, но имеют интервалы монотонности (какие?), разрывные (какие точки разрыва имеют эти функции?). Область определения и область значений этих функций:
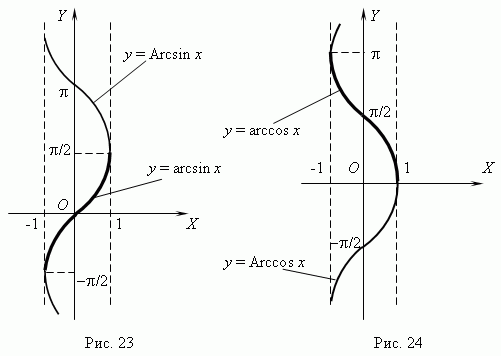
Функции y = Arcsin x (рис.23) и y = Arccos x (рис.24)многозначные, неограниченные; их область определения и область значений соответственно: 1 рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами: - у обеих функций одна и та же область определения: 1 их области значений: - функции ограниченные, непериодические, непрерывные и монотонные (y = arcsin x – возрастающая функция; y = arccos x – убывающая); - каждая функция имеет по одному нулю (x = 0 у функции y = arcsin x и x = 1 у функции y = arccos x).
Функции y = Arctan x (рис.25) и y = Arccot x (рис.26)- многозначные, неограниченные функции; их область определения:
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства: - у обеих функций одна и та же область определения: их области значений: - функции ограниченные, непериодические, непрерывные и монотонные (y = arctan x – возрастающая функция; y = arccot x – убывающая); - только функция y = arctan x имеет единственный ноль (x = 0); функция y = arccot x нулей не имеет. Композиция функций Если даны два отображения
Рис.1.30.Сквозное отображение
Таким образом, Пример 1.18 Пусть
Упражнение 1.3 Покажите, что если заменить множество Пример 1.19 Пусть Замечание 1.5 Даже если для функций Пример 1.20 Пусть Применяя композицию функций, которые сами могут получаться как композиции, мы можем получать сложные функции вида
Вопрос33 Взаимно-однозначное соответствие между множествами. Обратное правило и обратная функция. Графики взаимно обратных функций. Определения, свойства и графики гиперболических функций. (тут уже начинается вынос мозга) Мощностью конечного множества (множества, содержащего конечное число элементов) называется количество его элементов. Мощность множества A обозначается m (A). Пример 1 Определите мощность множества A = {1, 3, 5, 7, 9} нечётных чисел. Показать решение Простым пересчётом элементов убеждаемся, что нечётных чисел всего 5, и потому m (A) = 5. Ответ. 5. Ясно (да ну!), что понятие мощности конечных множеств позволяет сравнивать их по количеству элементов. Так, если A = {1, 3, 5, 7, 9}, а B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и потому m (A) > m (B). Однако если мы имеем дело с бесконечными множествами, то пересчитать элементы множества уже не удастся. Но иногда можно, как говорят, установить взаимно однозначное соответствие между двумя бесконечными множествами.
Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если из элементов этих множеств можно составить пары (a, b), причем каждый элемент из A и каждый элемент из B входят в одну и только одну пару. Множества, между которыми установлено взаимно однозначное соответствие, содержат одинаковое количество элементов.
Множества A и B называют равномощными, если между их элементами можно установить взаимно однозначное соответствие (ещё говорят: можно установить взаимно однозначное отображение множеств). Мощность множества натуральных чисел обозначается א. Алеф א – первая буква еврейского алфавита, так обозначается наименьшая возможная для бесконечных множеств мощность.
Множества, равномощные множеству натуральных чисел, называются счётными множествами. Пример 2 Множество натуральных чисел равномощно множеству нечётных чисел, так как между ними можно установить взаимно однозначное соответствие, например, по следующему правилу: 1 2 3... n... ↕ ↕ ↕ ↕ 1 3 5... 2 n – 1... Так как множество нечётных чисел является подмножеством натуральных чисел, то этот пример показывает, что бесконечное множество может быть равномощно своему подмножеству. Пример 3 Множество положительных рациональных чисел счётно. Действительно, если представить каждое рациональное число в виде несократимой дроби и записать его в следующую таблицу, а затем пронумеровать, как указано на рисунке, то окажется, что множество рациональных положительных чисел действительно счётно.
Рисунок 4.1.2.1.
Пример 4 Любой отрезок [ a; b ] равномощен отрезку [0; 1]. Взаимно однозначное соответствие между ними устанавливает формула y = (b − a) · x + a, где x Пример 5 Множества A Существуют и другие бесконечные множества, мощность которых больше, чем мощность счётных множеств. Так, множество всех точек отрезка [0; 1] не равномощно множеству натуральных чисел Как было показано в примере 4, множество всех точек отрезка [0; 1] равномощно множеству точек отрезка любой длины. Легко показать равномощность множеств отрезка [ a; b ] и интервала (a; b), а также отрезка [ a; b ] и луча (a; +∞). Наконец, можно доказать равномощность множеств всех точек отрезка и квадрата. Мощность множества всех действительных чисел (или, что то же, множества всех точек числовой оси) обозначается символом c («континуум»). Поскольку множество всех действительных чисел несчётно, то א < c. Континуум – не самая большая из бесконечных мощностей. Так, мощность множества всех подмножеств точек числовой оси больше, чем мощность самого множества всех точек оси. Она обозначается 2 c и называется гиперконтинуумом.
Обратная функция. Теорема о существовании и непрерывности обратной функции. f−1(f(x))=f(f−1(x))=x.
Монотонные функции и их свойства. Существование и непрерывность обратной функции. Теорема 1. Если функция y=f(x) строго возрастает (убывает) на множестве X, то для нее существует обратная функция x=f−1(y), которая определена на множестве Y=f(X) и является на Y строго возрастающей (убывающей). Доказательство. По условию функция f строго возрастает на множестве X. Это значит для любых x1,x2∈X и x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f−1:Y→X. Покажем, что функция f−1 строго возрастает на множестве Y. Пусть y1 и y2- любые точки из Y и y1<y2. Докажем, что x1=f−1(y1)<x2=f−1(y2). Допустим, чтоx1≥x2. По условию функция f строго возрастает на X, поэтому из условия x1≥x2 вытекает неравенствоy1=f(x1)≥y2=f(x2), что противоречит условию y1<y2. Т.о., условие строгой монотонности функции является достаточным для существования обратной функции.
Теорема 2. Если функция y=f(x) строго возрастает (убывает) и непрерывна на промежутке I, то существует обратная функция x=f−1(y), которая определена на промежутке Ef=f(I) и является на Е, строго возрастающей (убывающей) и непрерывной. Доказательство. Для определенности предположим, что функция f строго возрастает на промежутке I. По следствию из 2-ой теоремы Больцано-Коши область значений Ef=f(I) непрерывной функции f тоже есть промежуток. В силу строгого возрастания функции f для каждого y∈E существует единственная точка x∈I такая, что f(x)=y. Следовательно для функции f существует обратная функция f−1 определенная на промежутке Е и с множеством значений I. Покажем, что f−1 строго возрастает на Е. Пусть y1 и y2-- две произвольные точки из Е, такие, что y1<y2 и прообразами этих точек будут точки x1и x2. f−1(y1)=x1, и f−1(y2)=x2. Поскольку f - строго возрастающая функция, то неравенство y1=f(x1)<f(x2)=y2 возможно тогда и только тогда когда x1<x2 или тоже самое, когда f−1(y1)<f−1(y2). В силу произвольности y1 и y2 ∈E делаем вывод, что функция f−1 - строго возрастает на множестве Е. Что и требовалось доказать. 1. Гиперболическими синусом, косинусом, тангенсом и котангенсом называются функции:
ch(x± y)=chx · chy ± shx · shy, (1) sh(x± y)=shx · chy± chx · shy, (2) ch2x–sh2x=1, (3) ch2x=ch2x+sh2x, (4) sh2x=2shx · chx. (5) Тождества (2) и (5) аналогичны соответствующим формулам тригонометрии, а формулы (1), (3) и (4) отличаются от тригонометрических только знаком. Доказываются тождества (1) – (5) непосредственной проверкой. Более подробно о тождествах для гиперболических функций изложено в разделе III.
2. Рассмотрим уравнение гиперболы:
Его можно записать в параметрическом виде, используя гиперболические функции (этим и объясняется их название). Обозначим y= b·sht, тогда х2 / а2=1+sh2t =ch2t. Откуда x=± a·cht.
x= ± a ·cht,
Рис. 1. Знак ''+'' в верхней формуле (6) соответствует правой ветви гиперболы, а знак ''– '' - левой (см. рис. 1). Вершинам гиперболы А(– а; 0) и В(а; 0) соответствует значение параметра t=0.
2) (chx)'=shx (показывается аналогично).
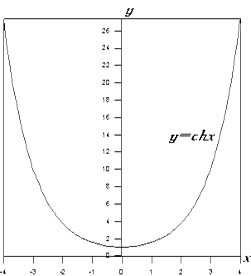
4) Здесь так же прослеживается определенная аналогия с тригонометрическими функциями. Полная таблица производных всех гиперболических функций приведена в разделе IV. 6. Нетрудно вычислить вторые производные основных гиперболических функций: 1) 2) 3) 4) 7. Используя результаты п. 1-6, строим графики основных гиперболических функций:
Вопрос34. Числовая последовательность. Предел числовой последовательности (конечный и бесконечный). Геометрическая иллюстрация. Теорема о сходимости монотонной и ограниченной последовательности.
Последовательность — это пздц (набор) элементов некоторого множества: для каждого натурального числа можно указать элемент данного множества; это число является номером элемента и обозначает позицию данного элемента в последовательности; для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности. Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма. Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность. В математике рассматривается множество различных последовательностей: числовые последовательности; временные ряды как числовой, так и не числовой природы; последовательности элементов метрического пространства последовательности элементов функционального пространства последовательности состояний систем управления и автоматов. Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей. Определение Пусть задано некоторое множество X элементов произвольной природы. Всякое отображение Образ натурального числа n, а именно, элемент xn = f (n), называется n -ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом. Связанные определения Подмножество Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется подпоследовательностью заданной последовательности.
Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины. Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел. Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений. [1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.
|

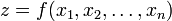 - вещественная функция n переменных.
- вещественная функция n переменных. ). Каждой точке функции сопоставим вектор:
). Каждой точке функции сопоставим вектор:  . Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
. Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
 , тангенс которого равен k: tan
, тангенс которого равен k: tan 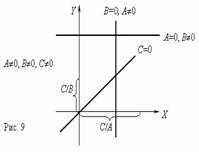
 График обратной пропорциональности – гипербола (рис.10). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью (о конических сечениях см. раздел «Конус» в главе «Стереометрия»). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
График обратной пропорциональности – гипербола (рис.10). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью (о конических сечениях см. раздел «Конус» в главе «Стереометрия»). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k. 0, область значений: y
0, область значений: y 

 Основные характеристики и свойства квадратной параболы:
Основные характеристики и свойства квадратной параболы: < x +
< x +  R), а область
R), а область Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает. Основные характеристики и свойства показательной функции:
Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает. Основные характеристики и свойства показательной функции: Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график (рис.18) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график (рис.18) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
 2
2
 y
y 


 и
и  , где
, где  , то имеет смысл "сквозное отображение"
, то имеет смысл "сквозное отображение" 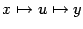 из
из  в
в  , заданное формулой
, заданное формулой  ,
,  , которое называется композицией функций
, которое называется композицией функций 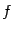 и
и  и обозначается
и обозначается  .
.
 ,
,  при всех
при всех  "сложено" из отображений
"сложено" из отображений  и
и  ).
). ,
,  , и
, и  ,
,  . Тогда
. Тогда 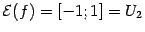 , и определена композиция
, и определена композиция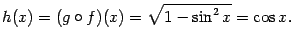
 , то композиция
, то композиция  , а не
, а не  .
. ,
, 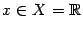 , и
, и  ,
,  . Тогда определена композиция
. Тогда определена композиция  , заданная формулой
, заданная формулой  . По известной формуле приведения полученная композиция -- это косинус:
. По известной формуле приведения полученная композиция -- это косинус:  при всех
при всех 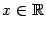 .
.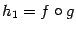 и
и 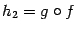 (что бывает далеко не для любой пары функций
(что бывает далеко не для любой пары функций  и
и 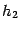 не обязаны совпадать; как правило, это не так.
не обязаны совпадать; как правило, это не так. и
и  ,
,  . Тогда
. Тогда  , а
, а  . Очевидно, что это разные функции:
. Очевидно, что это разные функции:  при всех
при всех  принимает значение
принимает значение  , например, при
, например, при  .
. и более длинные композиции.
и более длинные композиции. 1
1 [0; 1], y
[0; 1], y 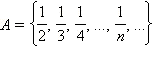 и
и  счётны и потому равномощны. В самом деле, установим взаимно однозначное соответствие между ними по следующему правилу:
счётны и потому равномощны. В самом деле, установим взаимно однозначное соответствие между ними по следующему правилу:

 ...
...  ... ↕ ↕ ↕ ↕ ↕ ↕ ↕ N 1 2 3... n... ↕ ↕ ↕ ↕ ↕ ↕ ↕ B 0
... ↕ ↕ ↕ ↕ ↕ ↕ ↕ N 1 2 3... n... ↕ ↕ ↕ ↕ ↕ ↕ ↕ B 0  ...
...  ...
... доказательство этой теоремы принадлежит немецкому математику Георгу Кантору.
доказательство этой теоремы принадлежит немецкому математику Георгу Кантору.
 ;
;  ;
;  .
.
 < t <
< t < 
 t
t  .
.

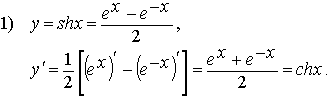









 из множества натуральных чисел
из множества натуральных чисел  в заданное множество X называется последовательностью (элементов множества X).
в заданное множество X называется последовательностью (элементов множества X). множества X, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
множества X, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.


