ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Вектор Итак, пусть прямая l проходит через точку М 1(x 1, y 1, z 1), лежащую на прямой параллельно вектору Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что Векторы Запишем это уравнение в координатной форме. Заметим, что Полученные уравнения называются параметрическими уравнениями прямой. При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой. Уравнение прямой, проходящей через две различные точки на плоскости Если прямая проходит через две точки A(x1, y1) и B(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2 то уравнение прямой можно найти, используя следующую формулу
Вопрос 20. Матрица размеров mxn. Квадратная матрица. Частные случаи (треугольная, диагональная, скалярная, единичная матрицы). Линейные операции над матрицами (сложение и умножение на число) и их свойства. Умножение двух матриц. Свойства операции умножения матриц. Ответ: Любая прямая, перпендикулярная плоскости, называется нормалью к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектором плоскости. Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля. Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно. Ур.плоскости через нормальный вектор
Общее уравнение плоскости
Частные случаи общего уравнения плоскости: 1) By + Cz + D = 0 - параллельна оси Ox; 2) Ax + Cz + D = 0 - параллельна оси Oy; 3) Ax + By + D = 0 - параллельна оси Oz; 4) Cz + D = 0 - параллельна оси Oxy; 5) By + D = 0 - параллельна оси Oxz; 6) Ax + D = 0 - параллельна оси Oyz; 7) Ax + By + Cz = 0 - проходит через начало координат; 8) By + Cz = 0 - проходит через ось Ox; 9) Ax + Cz = 0 - проходит через ось Oy; 10) Ax + By = 0 - проходит через ось Oz; 11) z = 0 - плоскость Oxy; 12) y = 0 - плоскость Oxz; 13) x = 0 - плоскость Oyz.
Векторное уравнение плоскости Пусть r -- радиус-вектор текущей точки Взаимное расположение двух плоскостей Если 1) пересекаются 2) параллельны (но не совпадают) 3) совпадают Если плоскости заданы уравнениями 1)
2) 3)
Вопрос21 Уравнение плоскости, проходящей через данную точку, параллельно 2м неколлинеарным векторам. Уравнение плоскости, проходящей через 3 данные точки. Уравнение плоскости «в отрезках». Нормальное уравнение плоскости. Уравнение плоскости по точке и двум неколлинеарным векторам В векторном виде
В координатах
Уравнение плоскости по трем точкам В векторном виде
В координатах
или
Уравнение плоскости в отрезках
где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.
где Приведение общего уравнения плоскости к нормальному виду:
Здесь
Вопрос22 Различные виды уравнений прямой в пространстве (параметрические, канонические, через 2 точки, общие) Направляющий вектор прямой, заданной общими уравнениями.
Уравнения прямой по двум точкам
Векторно-параметрическое уравнение прямой
где
Канонические уравнения прямой
|

 Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора  , параллельного этой прямой.
, параллельного этой прямой. .
. .
. и
и  коллинеарны, поэтому найдётся такое число t, что
коллинеарны, поэтому найдётся такое число t, что  , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через
, где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через  и
и  , получаем
, получаем  . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.
. Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.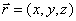 ,
,  и
и  отсюда
отсюда 


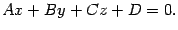
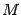 плоскости
плоскости  ,
, 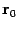 -- радиус-вектор точки
-- радиус-вектор точки  . Тогда уравнение (11.2) можно переписать в виде
. Тогда уравнение (11.2) можно переписать в виде 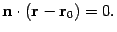 Такое уравнение обычно называют векторным уравнением плоскости
Такое уравнение обычно называют векторным уравнением плоскости  , то они:
, то они:


 и
и  то случаи 1 - 3 имеют место, когда:
то случаи 1 - 3 имеют место, когда:









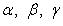 - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.
- углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.
 - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если
- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если  произвольно, если D = 0.
произвольно, если D = 0.

 - фиксированная точка, лежащая на прямой;
- фиксированная точка, лежащая на прямой;  - направляющий вектор.
- направляющий вектор.



