Билет 7
1. Базис и система координат на плоскости и в пр-ве Ответ: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов Любой вектор плоскости Также говорят, что вектор Иными словами, говоря о разложении по базису мы подразумеваем какие-то коэффициенты, которые соответствуют векторам.
1.1 Система координат на плоскости
Ответ: Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и размерность по осям. Прямоугольную систему координат вполне можно определить через ортонормированный базис Точка Думаю, всем понятно, что с помощью точки Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку
1.2. Система координат в пр-ве Ответ: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов Напоминаю, также можно сказать, что вектор Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов: Точка
Точка
2. Геометрические и алгебраические проекции вектора на ось
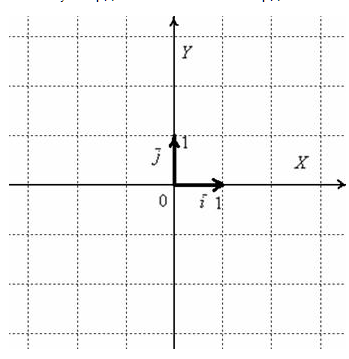
3. Координаты вектора на плоскости и в пространстве Начну с векторов на плоскости. Изображаем декартову с.к. и откладываем единичные вектора.
Векторы Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице. Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: Ответ: Любой вектор
|

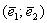 , взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.
, взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.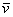 единственным образом раскладывается по базису
единственным образом раскладывается по базису  , где
, где 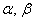 – действительные числа. Числа
– действительные числа. Числа 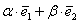 называют разложением вектора
называют разложением вектора 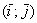 . И это почти так. Формулировка звучит следующим образом:
. И это почти так. Формулировка звучит следующим образом: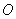 плоскости, которая называется началом координат, и ортонормированный базис
плоскости, которая называется началом координат, и ортонормированный базис 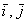 .
.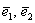 произвольной ненулевой длины. Собственно пример данной системы, всем известной:
произвольной ненулевой длины. Собственно пример данной системы, всем известной: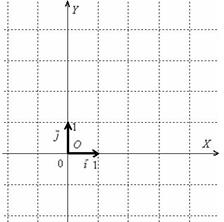
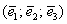 , взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису
, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису 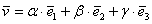 , где
, где 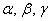 – координаты вектора
– координаты вектора  , взятые в определённом порядке, задают аффинную систему координат трёхмерного пространства:
, взятые в определённом порядке, задают аффинную систему координат трёхмерного пространства: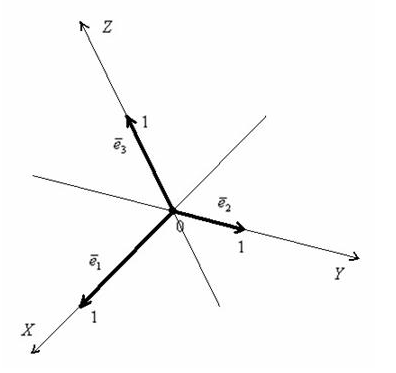
 задают декартову прямоугольную систему координат пространства.:
задают декартову прямоугольную систему координат пространства.: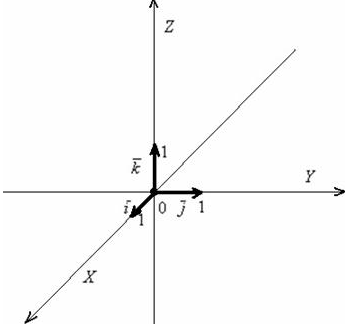
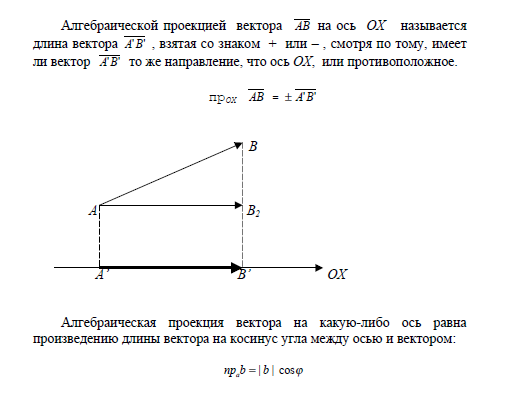
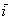 и
и 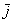 ортогональны. Ортогональны = Перпендикулярны.
ортогональны. Ортогональны = Перпендикулярны.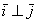 .
.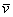 плоскости единственным образом выражается в виде:
плоскости единственным образом выражается в виде: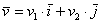 , где
, где 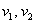 – числа, которые называются координатами вектора в данном базисе. А само выражение
– числа, которые называются координатами вектора в данном базисе. А само выражение 


