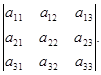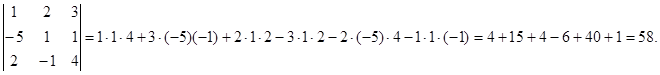Билет 2. Ответ: Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы
Ответ: Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
Квадратная матрица называется вырожденной, если её определитель равен нулю. Квадратная матрица называется невырожденной, если её определитель отличен от нуля. Определитель произведения квадратных матриц равен произведению определителей сомножителей.
Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.
Обозначение:
Пример. Для
Алгебраическим дополнением
Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры.
1.
Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:
1. 2.
|

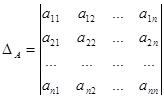
 выбранный элемент определителя,
выбранный элемент определителя, 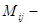 его минор.
его минор.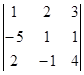
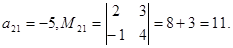
 элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.
элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е. 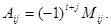
 .
.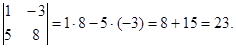 2.
2. 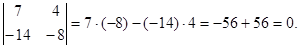
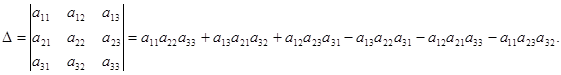












 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: