Непрерывность функции в точке. Теорема. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Теорема. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Тот же факт можно записать иначе:
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва. Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию верно неравенство
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x) где a(х) – бесконечно малая при х=х0.
Производная функции, таблица производных Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Операция нахождения производной функции называется дифференцированием. В результате выполнения этой операции мы по определенным правилам получаем другую функцию:
В этом равенстве
Для того, чтобы каждый раз не искать производные элементарных функций, используя определение производной, существует таблица производных элементарных функций: 1. Производная константы равна нулю:
2. Производная степенной функции:
Заметим, что Примеры. 1. 2. 3. 3. Производная показательной функции:
Пример.
Частный случай этой формулы:
4. Производная логарифма:
Частный случай этой формулы:
5. Производные тригонометрических функций:
6. Производные обратных тригонометрических функций:
|


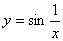

 .
.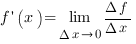

 – функция, от которой мы берем производную,
– функция, от которой мы берем производную, – функция, которая получается в результате этой операции.
– функция, которая получается в результате этой операции.
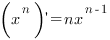
 может принимать любые действительные значения.
может принимать любые действительные значения.


















