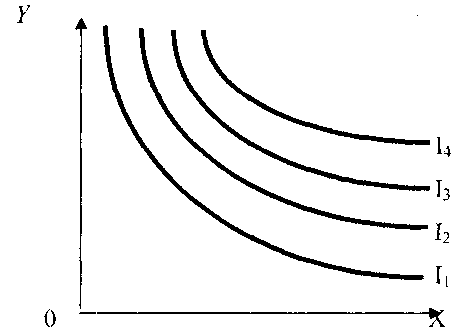
Свойства кривых безразличия
Отметим свойства кривых безразличия: 1) Кривая безразличия имеет отрицательный наклон, то есть проходит вниз слева направо. Доказательство: предположим противное, то есть, что кривая безразличия идет вверх слева направо. Значит каждый набор, соответствующий точке, расположенной на кривой выше, будет содержать большее количество каждого блага, чем нижний. Это противоречит предположению 3. Для описания предпочтений индивида по всем наборам благ Х и Y, используют изображение семейства кривых безразличия, которое называется картой безразличия (рис. 4-3):
На графике изображены четыре кривых безразличия, которые представляют часть карты безразличия. Кривая I4 соответствует наивысшему уровню удовлетворения, следуя за кривыми I3, I2, I1. 2) Кривые безразличия не могут пересечься (доказать самостоятельно). 3) Кривая безразличия может быть проведена через каждую точку в пространстве благ (это следует из предположения 1) 4) Рассмотрим одну из кривых безразличия (рис. 4-4):
Пусть отрезок х1х2 равен отрезку х3х4, тогда при переходе из точки А в точку В потребитель сохранил общую полезность набора благ при увеличении потребления блага Х на Dх1 и уменьшении потребления блага Y на Dу1. При переходе из С в D потребитель сохранил общую полезность при увеличении потребления блага Х на Dх2 = Dх1 и уменьшении потребления блага Y на Dу2, при этом Dу1 > Dу2.
|