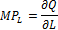Производственная функция в коротком периоде
Поскольку в коротком периоде переменным является только фактор производства «труд», то можно записать Q =f(L)и рассматривать производственную функцию как функцию одного аргумента (рис. 5-2)

Производственная функция делит координатную плоскость на два множества: недостижимые и неэффективные комбинации объемов используемого труда и объемов производства блага. Сама функция, как уже говорилось, характеризует эффективные сочетания (Q, L). На функции можно выделить три участка: на первом (до точки А) объем выпуска растет более высокими темпами, чем объем используемого труда. Этот участок характеризует состояние недоиспользования существующих (фиксированных!) объемов капитала. В точке А наблюдается технологически оптимальное соотношение труда и капитала. Второй участок (от точки А до точки В) показывает, что объем выпуска растет более медленными темпами, чем объем используемого труда. Этот участок характеризует закон убывающей предельной производительности фактора производства (труда): Если количества некоторых факторов фиксированы, то предельный продукт любого переменного фактора будет по достижении некоторого объема выпуска убывать по мере увеличения затрат данного фактора. На третьем участке (после точки В) показано, что объем выпуска убывает с ростом количества переменного фактора. Обоснование такой формы производственной функции может быть следующим: первые единицы ресурса (работники) являются дефицитными, поэтому увеличение их количества в сочетании с фиксированными избыточными объемами других ресурсов (капитала) приводит к возрастающей отдаче до тех пор, пока не будет достигнута некоторая оптимальная комбинация ресурсов (к примеру, любой технологический процесс рассчитан на определенное число исполнителей). При дальнейшем увеличении переменного ресурса происходит перенасыщение этим ресурсом, что приводит к замедляющемуся увеличению объемов выпуска. Для описания производственной функции в коротком периоде используется ряд показателей, называемых характеристиками технологической результативности производства (табл. 5-1). Таблица 5-1 Характеристики технической результативности производства в коротком периоде
Из формулы среднего продукта (см. табл. 5-1) видно, что величина среднего продукта определится как тангенс угла наклона касательной в каждой точке производственной функции. Продемонстрируем взаимное расположение кривых совокупного, среднего и предельного продуктов (рис. 5-3). Взаимосвязь между совокупным, средним и предельным продуктами проявляется в следующем: • при увеличении переменного фактора L совокупный продукт растет, если значения предельного продукта MPL положительны, и снижается, когда значения предельного продукта отрицательны; • при росте совокупного продукта TPL значения предельного продукта MPL всегда положительны, а при снижении — отрицательны; • совокупный продукт TPL достигает максимума, когда предельный продукт MPL равен нулю; • средний продукт от переменного фактора APL растет до тех пор, пока его значения ниже значений предельного продукта MPL, и снижается, если они выше значений предельного продукта; • в случае равенства значений среднего APL и предельного продуктов MPL средний — достигает своего максимума.
Можно выделить три стадии использования переменного ресурса в производстве в коротком периоде. На первой стадии привлечение каждой дополнительной единицы ресурса приводит к увеличению не только общего, но и среднего продукта. Однако эта стадия неэффективна для фирмы, поскольку каждая следующая единица ресурса используется более эффективно, чем предыдущая. Оптимальной для фирмы является вторая стадия, на которой средний продукт уменьшается, но каждая дополнительно привлекаемая единица продолжает приносить дополнительный продукт. В какой точке этой стадии остановится фирма, определяется соотношением цен на ресурс и на благо. Третья стадия характеризуется уменьшением выпуска с увеличением используемого ресурса и является нерациональной.
|

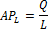
 или
или