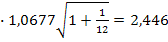Задача № 7. Упрощенные приемы прогнозирования
Упрощенные приемы прогнозирования. Прибыть за год характеризуется данными, приведенными в таблице 1.
Оценим существенность различий в дисперсиях: F=0,92/0,86=1,07 при табличном значении 5,05 (для а =0,05 и при числе степеней свободы 5 и 5). Дисперсии можно признать равными. Тогда оценим существенность расхождения в среднемесячных уровнях прибыли за каждое полугодие по t-критерию Стьюдента:
Произведя дальнейшие вычисления, находим, что t= 1,84. Это меньше i т= 2,23. Следовательно, с вероятностью 0,95 можно признать, что тенденции в ряду динамики нет. Прогноз по стационарному ряду основан на предположении о неизменности в будущем среднего уровня динамического ряда, т.е. yp=
где yp - прогнозное значение. Так как средний уровень динамического ряда имеет погрешность как выборочная средняя и, кроме того, отдельные уровни ряда колеблются вокруг среднего значения, принято прогноз давать в интервале:
где
n- длина динамического ряда.
где дисперсия.
ta=0,05,n-1=11=2,201 Тогда ошибка прогноза составит: 2,201 Соответственно прогноз прибыли на январь следующего года окажется таким: 61
|
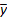, прибыль, тыс.руб.
2
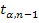- табличное значение t-критерия Стьюдента при уровне значимости а числе степеней свободы (n-1). Для нашего примера:
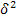- межгрупповая дисперсия; 
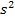- внутригрупповая
и 
