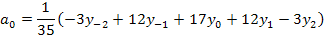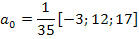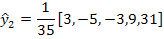Задача № 2. Методы сглаживания временных рядов.
Методы сглаживания временных рядов. По данным об урожайности (табл. 1) за 16 лет рассчитайте: трех-, семилетние скользящие средние и графически сравните результаты; пятилетнюю взвешенную скользящую среднюю. Таблица1. Урожайность пшеницы, ц/га
Решение: 1. Результаты расчетов представлены в табл.2. Таблица 2. Расчет скользящих средних
При трехлетней скользящей средней (i=3)
При семилетней скользящей средней (i=7)
2. Для вычисления значений пятилетней взвешенной скользящей средней воспользуемся таблицей 1. Тогда
И т.д. Задача № 3, Пусть сглаживание осуществляется по пятичленной скользящей средней (I=5), причем аппроксимация осуществляется квадратичным полиномом (m=2). Требуется определить весовые коэффициенты для восстановления двух последних уровней рада. Решение: Осуществим перенос начала координат в середину активного участка: t=-2;-1;0;+1;+2; После этого система нормальных уравнений примет вид:
Из первого и третьего уравнений определим выражение для коэффициента a0:
или в символической записи Выразим теперь остальные неизвестные параметры из системы уравнений (1.8.54):
s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Полученные выражения для коэффициентов a0,a1,a2, подставим в уравнение сглаживающего квадратического полинома:
Последовательно подставляя в это выражение t=1;2, получим весовые коэффициенты для восстановления последних уровней ряда: - при t=l (восстановление предпоследнего уровня ряда)
-при t=2(восстановление последнего уровня ряда)
Если последними пятью уровнями ряда были 0; 1; 4; 9; 16, то восстановление двух последних значений осуществлялось бы следующим образом: - при t=1
-при t=2
|

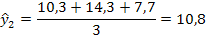
 и т.д.
и т.д.
 и т.д.
и т.д.

 (1.8.53)
(1.8.53)