Методы аналитического выравнивания и прогнозирования временных рядов.
Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:
где yt — уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t. Аналитическое выравнивание состоит в подборе для данного ряда динамики теоретической кривой, наилучшим образом описывающей эмпирические данные. Это могут быть различные функции: а) полиномы различных степеней: -первой степени
где ао, -второй
-третьей степени
б) показательная кривая
И другие. В тех случаях, когда требуется особо точное изучение тенденции развития (например, модели тренда для прогнозирования), при выборе вида адекватной функции можно использовать специальные критерии математической статистики. Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уровнями:
где
Параметры уравнения ai, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вытесняются выровненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней уь плавно изменяющимися уровнями, наилучшим образом аппроксимирующими статистические данные. Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней). Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны. Вопрос о возможности применения построенных моделей в целях анализа и прогнозирования явления может быть решен только после проверки адекватности, т.е. соответствия модели исследуемому процессу. На практике при проведении сравнительной оценки моделей может использоваться такая характеристика, как средняя квадратическая ошибка (S):
где n- длина временного ряда;
Часто знаменателем подкоренного выражения служит величина (n-k), где к — число оцениваемых коэффициентов модели. Экстраполяция в радах динамики Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования, т.е. для определения ориентировочных размеров явлений в будущем. Для этого используют метод экстраполяции. Под экстраполяцией понимают нахождение уровней за пределами изучаемого рада, т.е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция). Поскольку в действительности тенденция развития не остается неизменной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки. Экстраполяцию рядов динамики осуществляют различными способами, например, экстраполируют ряды динамики выравниванием по аналитическим формулам. Зная уравнение для теоретических уровней и подставляя в него значения t за пределами исследованного рада, рассчитывают для t вероятностные (прогнозные) На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками. Для определения границ интервалов используют формулу:
где ta- табличное значение t критерия Стьюдента с n-1 степенями свободы и уровнем вероятности «р»;
Значение ее определяется по формуле 1 - период упреждения. В свою очередь среднее квадратическое отклонение S для выборки равно:
Где n — число уровней ряда динамики; Полученный доверительный интервал учитывает неопределенность, которая связана с оценкой средней величины, и его применение для прогнозирования увеличивает степень надежности прогноза» Таким образом, вероятностные границы интервала прогнозируемого явления:
|

 (1.8.26)
(1.8.26) (1.8.27)
(1.8.27)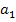 — параметры уравнения; t — время;
— параметры уравнения; t — время;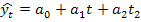 (1.8.28)
(1.8.28)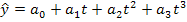 (1.8.29)
(1.8.29)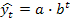 (1.8.30)
(1.8.30) (1.8.31)
(1.8.31)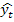 — выровненные (расчетные) уровни;
— выровненные (расчетные) уровни; — фактические уровни.
— фактические уровни.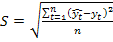 (1.8.32)
(1.8.32) - фактическое значение уровня рада.
- фактическое значение уровня рада. (1.8.33)
(1.8.33)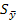 - средняя квадратическая ошибка средней.
- средняя квадратическая ошибка средней.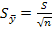
 (1.8.34)
(1.8.34) (1.8.35)
(1.8.35)


