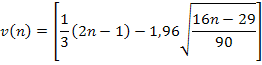Проверка гипотезы о существовании тренда
Решение любой задачи по анализу и прогнозированию временных рядов начинается с построения графика исследуемого показателя, тем более что современные программные средства предоставляют для этого большие возможности. При этом не всегда четко прослеживается присутствие тренда во временном ряду. В этих случаях прежде чем перейти к определению тенденции и выделению тренда, нужно выяснить, существует ли вообще тенденция в исследуемом процессе. Основные подходы к решению этой задачи основаны на статистической проверке гипотез. Критерии выявления компонент ряда основаны на проверке гипотезы о случайности ряда, т.е. по существу на статистической проверке гипотезы: H0:My(t)=a=const; (1.8.22) На практике чаще всего используется, так называемый, критерий «восходящих и нисходящих» серий. Его применение может быть представлено в виде следующей последовательности шагов. 1. На первом шаге образуется последовательность
В случае, когда последующее наблюдение окажется равным предыдущему, учитывается только одно наблюдение. Таким образом, элементы этой последовательности принимают значение «+», если последующее значение уровня ряда больше предыдущего, и «-», если последующее значение уровня ряда меньше предыдущего. Общее число знаков «+» и «-» заранее неизвестно. Индекс I может принимать значения 1,2,...K, где K≤n-1. 2. Подсчитывается v(n) - число серий в совокупности,
imax(n)<i0(n), где i0(n) —табличное значение, зависящее от n-длины временного ряда. Таблица значений i0(n) критерия «восходящих и нисходящих» серий
Если хотя бы одно из неравенств нарушается, то нулевая гипотеза о случайности ряда отвергается (следовательно, подтверждается наличие зависящей от времени неслучайной составляющей).
|

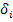 из плюсов и минусов по следующему правилу:
из плюсов и минусов по следующему правилу: (1.8.23)
(1.8.23)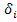 где под серией понимается последовательность, подряд идущих плюсов и минусов. Один плюс или один минус тоже будут считаться серией. Очевидно, что при этом каждая серия, состоящая из плюсов, соответствует возрастанию уровней ряда ("восходящая " серия), а последовательность минусов - их убыванию ("нисходящая" серия). Определяется imax(n) - протяженность самой длинной серии. Для того, чтобы не была отвергнута гипотеза о случайности ряда должны выполняться следующие неравенства (при уровне значимости а, заключенным между 0,05 и 0,0975):
где под серией понимается последовательность, подряд идущих плюсов и минусов. Один плюс или один минус тоже будут считаться серией. Очевидно, что при этом каждая серия, состоящая из плюсов, соответствует возрастанию уровней ряда ("восходящая " серия), а последовательность минусов - их убыванию ("нисходящая" серия). Определяется imax(n) - протяженность самой длинной серии. Для того, чтобы не была отвергнута гипотеза о случайности ряда должны выполняться следующие неравенства (при уровне значимости а, заключенным между 0,05 и 0,0975):