Упрощенные приемы прогнозирования
Временной ряд называется стационарным, если в нем отсутствует тенденция развития. Это значит, что уровни динамического ряда варьируют вокруг среднего уровня, отклонения от которого представляет собой случайную колеблемость. Модель уровня динамического ряда в этом случае имеет вид:
где yt - уровни динамического ряда;
Если стационарный ряд разбить на две равные по времени части, то средние уровни по этим частям не должны существенно различаться, т.е.
где n1=n2- число уровней в каждой половине динамического ряда;
В связи с тем, что число уровней динамического ряда у исследователя обычно ограничено, каждая половина ряда рассматривается как малая выборка, и дисперсия по ней определяется по формуле:
Сравнивая фактическое значение t-критерия с табличным при уровне значимости 0,05 и числе степеней свободы (n-2), различия между средними уровнями признаются несущественными, если t фактическое меньше табличного значения. В этом случае ряд можно считать стационарным. Прогноз по стационарному ряду основан на предположении о неизменности в будущем среднего уровня динамического ряда, т.е. yp= уровень динамического рада имеет погрешность как выборочная средняя и, кроме того, отдельные уровни ряда колеблются вокруг среднего значения, принято прогноз давать в интервале:
где n - длина динамического ряда;
|

 (1.8.38)
(1.8.38) - средний за период уровень динамического ряда;
- средний за период уровень динамического ряда; - случайная составляющая, определяемая как
- случайная составляющая, определяемая как
 =
=  Поскольку при практических расчетах полного равенства средних не бывает из-за колеблемости уровней, с помощью t-критерия Стьюдента дается оценка, существенно ли различаются между собой средние и можно ли их различие связывать только с действием случайности. Если в двух сравниваемых частях динамического ряда дисперсии уровней различаются несущественно, то проверка равенства средних уровней осуществляется по t-критерию Стьюдента по формуле:
Поскольку при практических расчетах полного равенства средних не бывает из-за колеблемости уровней, с помощью t-критерия Стьюдента дается оценка, существенно ли различаются между собой средние и можно ли их различие связывать только с действием случайности. Если в двух сравниваемых частях динамического ряда дисперсии уровней различаются несущественно, то проверка равенства средних уровней осуществляется по t-критерию Стьюдента по формуле: (1.8.39)
(1.8.39) - среднее квадратическое отклонение разности средних, которое может быть определено как корень из групповых дисперсий:
- среднее квадратическое отклонение разности средних, которое может быть определено как корень из групповых дисперсий: (1.8.40)
(1.8.40)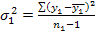 и
и  (1.8.41)
(1.8.41) (1.8.42)
(1.8.42)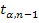 —табличное значение t-критерия Стьюдента при уровне значимости а и числе степеней свободы (n-1).
—табличное значение t-критерия Стьюдента при уровне значимости а и числе степеней свободы (n-1).


