Алгоритмы вычисления конечных сумм
Сегодня мы займемся вычислением различных числовых сумм, или, как принято говорить в математике, суммированием конечных числовых рядов. Думаю, что какая-то часть того, что я собираюсь рассказать, некоторым из вас известна, но надеюсь, что каждый увидит и услышит что-то новое. I. Начнем мы с вычисления сумм некоторых дробных выражений. Рассмотрим несколько примеров, в которых вы попытаетесь сначала сами найти способ вычисления, а если не получится, то будем рассуждать вместе. Пример 1. Вычислите сумму: Понятно, что приводить дроби к общему знаменателю – трудоемко и бесполезно. Заметим, что не случайно, знаменатели всех членов ряда заданы в виде произведений двух соседних натуральных чисел. При каких операциях с дробями нам приходится перемножать знаменатели? Чаще всего, при выполнении сложения или вычитания дробей. Так как числитель каждой дроби равен 1, то вряд ли мы сможем получить такую дробь путем сложения дробей, а вот вычитание дробей может привести к успеху. Действительно, обозначим искомую сумму S, тогда: S = Другими словами, мы вывели следующее соотношение: Обратите внимание, что в данном случае, n – натуральное, но полученное равенство Пример 2. Вычислите сумму: Ситуация похожая, поэтому имеет смысл попробовать сходный метод, то есть попытаться получить некоторое представление дроби, знаменатель которой является произведением трех последовательных натуральных чисел, в виде разности двух других дробей. Возникает гипотеза: Проверим ее, выполнив вычитание в правой части равенства. Увидим, что наша гипотеза неверна, но полученный результат сразу позволит ее скорректировать. Оказывается, что выполняется равенство: Обозначим искомую сумму S и воспользуемся полученным соотношением: S = Пример 3. Вычислите сумму: Сразу понятно, что прием, использованный уже дважды, здесь не поможет. При суммировании такого ряда чисел «срабатывает» другой метод, с которым мы еще встретимся в дальнейшем. Обозначим искомую сумму S и прибавим к ней дробь ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, Таким образом, S + Использованное нами соотношение в общем виде выглядит так: Пример 4. Вычислите сумму: Вычисление таких сумм, по-видимому, знакомо многим восьмиклассникам, но без этого примера «картина» будет явно не полной! В таких случаях выручает основное свойство дроби: можно умножить числитель и знаменатель каждого слагаемого на одно и то же число, отличное от нуля, а именно, на число, сопряженное знаменателю. Другими словами, можно использовать соотношение: Тогда, искомая сумма S равна: S = (– 1 + Отметим, что и в этом случае задание можно сформулировать в виде неравенства, попутно обобщив его, например, так: «Докажите, что для любого натуральногоn выполняется неравенство В заключение первой части лекции следует сказать, что при вычислении многих сумм можно поступать совсем по-другому. А именно, рассматривая частные случаи, пытаться угадать результат для случая n слагаемых, а затем доказывать полученную гипотезу, пользуясь методом математической индукции. Но это, как принято говорить, «совсем другая история». Для закрепления услышанного полезно самостоятельно выполнить несколько упражнений.
|

 .
.
 .
.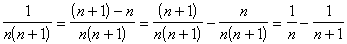 , которым и воспользовались.
, которым и воспользовались. справедливо для любых дробных выражений, знаменатель которых отличен от нуля!
справедливо для любых дробных выражений, знаменатель которых отличен от нуля! .
. .
. .
. =
=  =
=  .
. . (Напомню, что для любого натурального n его факториал – это произведение всех натуральных чисел от 1 до n,то есть n! = 1×2×...×(n – 1)n.)
. (Напомню, что для любого натурального n его факториал – это произведение всех натуральных чисел от 1 до n,то есть n! = 1×2×...×(n – 1)n.) , причем сложение начнем выполнять с конца. Последовательно получим:
, причем сложение начнем выполнять с конца. Последовательно получим: =
= 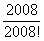 =
= 
 =
= 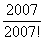 =
= 
 +
+  = 1
= 1 . Отметим также, что задание можно было сформулировать иначе: «Докажите, что сумма такого ряда меньше 1».
. Отметим также, что задание можно было сформулировать иначе: «Докажите, что сумма такого ряда меньше 1». .
. =
=  =
=  = – (
= – (  ) =
) =  .
. ) + (–
) + (–  ) +.... + (–
) +.... + (–  +
+  ) = –1 + 10 = 9.
) = –1 + 10 = 9. ».
».


