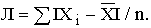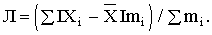Среднее линейное отклонение, его формулы.
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним. Для характеристики колеблемости признака используется ряд показателей. Один из показателей вариации: среднее линейное отклонение. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений: Порядок расчета среднего линейного отклонения следующий: 1) по значениям признака исчисляется средняя арифметическая; 2) определяются отклонения каждой варианты от средней; 3) рассчитывается сумма абсолютных величин отклонений; 4) сумма абсолютных величин отклонений делится на число значений. Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:
Порядок расчета среднего линейного отклонения взвешенного следующий: 1) вычисляется средняя арифметическая взвешенная; 2) определяются абсолютные отклонения вариант от средней; 3) полученные отклонения умножаются на частоты; 4) находится сумма взвешенных отклонений без учета знака; 5) сумма взвешенных отклонений делится на сумму частот:
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования.
|