Среднее квадратическое отклонение
§ Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение ( § Среднее квадратическое отклонение простое: § § Дисперсия § Дисперсия простая: § § В нашем примере: § Дисперсия взвешенная: § § Более удобно вычислять дисперсию по формуле: § § которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней. Относительные показатели вариации включают: § Коэффициент осцилляции § Относительное линейное отклонение (линейный коэффициент варианции) § Коэффициент вариации (относительное отклонение) Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:
44.Использование показателей вариации в статистическом анализе. Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. Термин «вариация» имеет латинское происхождение - variatio, что означает различие, изменение, колеблемость. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение. Для измерения вариации признака используют как абсолютные, так и относительные показатели. К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др. Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:
Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели. Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю. Формула среднего линейного отклонения (простая)
Формула среднего линейного отклонения (взвешенная)
Средняя квадратическая простая
Средняя квадратическая взвешенная
Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины. Формулы дисперсии взвешенной
Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах, особенно для целей сравнения колеблемости различных признаков одной и той же совокупности или для сравнения колеблемости одного и того же признака в нескольких совокупностях. Данные показатели рассчитываются как отношение размаха вариации к средней величине признака (коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака (линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака (коэффициент вариации) и, как правило, выражаются в процентах. Формулы расчета относительных показателей вариации:
где VR - коэффициент осцилляции; 45.Понятие о ряде динамики. Виды рядов динамики. Их задачи. Важнейшая задача статистики – изучение социально-экономических явлений общественной жизни во времени. Изменение этих явлений, т.е. выявление закономерности развития изучаемого явления, статистика исследует путем построения и анализа рядов динамики. Ряды динамики – это статистические данные, отображающие развитие во времени изучаемого явления. Их также называют хронологическими или временными рядами. В каждом ряду динамики имеется два основных элемента: 1) показатель времени – t; 2) соответствующие им уровни развития изучаемого явления – y. В качестве показателей времени в рядах динамики выступают определенные даты (моменты), т.е. отдельные периоды (годы, кварталы, месяцы, пятилетка). Уровни рядов динамики отображают количественную оценку развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами. Ряды динамики различаются по следующим признакам: 1. По времени отражения уровней в динамических рядах. В зависимости от характера изучаемого явления уровни рядов динамики могут относиться к определенным датам (моментам) времени и к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные. Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Таким образом, в моментном ряду динамики уровни рядов суммировать нельзя, а разность между показателями характеризует изменение явления за определенный период, в данном случае за год. С помощью моментных рядов динамики изучают состояние кадров, конкурентную среду, потребительские и другие показатели, отображающие состояние изучаемых явлений на отдельные даты (моменты) времени. Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные интервалы времени. Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени. С помощью интервальных рядов динамики изучают изменения во времени, представление и реализацию товаров и услуг, суммы издержек обращения и другие показатели, отображающие итоги изучаемого явления за отдельные периоды. Следующий классификационный признак рядов динамики это: 2. Форма выражения уровней рядов динамики. Они могут быть представлены абсолютными, относительными и средними величинами. Также они могут быть моментными или интервальными. В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла, так как относительные и средние величины являются производными и исчисляются через деление других величин. При составлении динамических рядов надо соблюдать следующее правило: уровни рядов должны быть сопоставимыми – это значит однородность показателей по экономическому содержанию, по территории.
|

 ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
 - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
- представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.



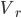





 (6.1)
(6.1)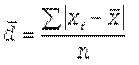
 При использовании показателя среднего линейного отклонения возникают определенные неудобства, связанные с тем, что приходится иметь дело не только с положительными, но и с отрицательными величинами, что побудило искать другие способы оценки вариации, чтобы иметь дело только с положительными величинами. Таким способом стало возведение всех отклонений во вторую степень. Обобщающие показатели, найденные с использованием вторых степеней отклонений, получили очень широкое распространение. К таким показателям относятся среднее квадратическое отклонение
При использовании показателя среднего линейного отклонения возникают определенные неудобства, связанные с тем, что приходится иметь дело не только с положительными, но и с отрицательными величинами, что побудило искать другие способы оценки вариации, чтобы иметь дело только с положительными величинами. Таким способом стало возведение всех отклонений во вторую степень. Обобщающие показатели, найденные с использованием вторых степеней отклонений, получили очень широкое распространение. К таким показателям относятся среднее квадратическое отклонение  и среднее квадратическое отклонение в квадрате
и среднее квадратическое отклонение в квадрате 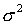 , которое называют дисперсией.
, которое называют дисперсией. (6.4)
(6.4) (6.5)
(6.5) и простой
и простой  :
: (6.6)
(6.6) (6.7)
(6.7) - линейный коэффициент вариации;
- линейный коэффициент вариации;  - коэффициент вариации.
- коэффициент вариации.


