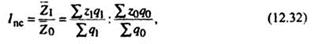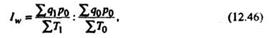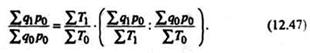Показатели динамики социально-экономических явлений.
47. Сопоставимость в рядах динамики. Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения или единиц счета. (Нельзя, например, сравнивать и анализировать цифры о производстве тканей, если за одни годы цифры даны в погонных метрах, а за другие - в квадратных метрах). На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей. (Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие - с убранной, то такие уровни будут несопоставимы). Условием сопоставимости уровней ряда динамики является периодизация динамики. Процесс выделения однородных этапов развития рядов динамики носит название периодизации динамики. Важно также, чтобы в ряду динамики интервалы, или моменты, по которым определены уровни, имели одинаковый экономический смысл. Условием сравнимости уровней интервального ряда является наличие равных интервалов, по которым даны уровни. Совершенно очевидно, что нельзя сравнивать квартальную продукцию с годовой. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое. Несопоставимость уровней ряда может возникнуть вследствие изменения территориальных границ областей, районов и т.д. Приведение уровней ряда к сопоставимому виду. Данный прием осуществляется методом смыкания рядов динамики. Под смыкаем понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам. Приведение рядов динамики к одному основанию. Т.е. к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему. Коэффициент опережения (замедления): 48.Средние показатели в рядах динамики. С течением времени изменяются не только уровни явлений, но и показатели их динамики – абсолютные приросты и темпы развития. Поэтому для обобщающей характеристики развития, для выявления и измерения типичных основных тенденций и закономерностей и решения других задач анализа используются средние показатели временного ряда: средние уровни, средние абсолютные приросты и средние темпы динамики. К расчету средних уровней ряда динамики часто приходится прибегать уже при построении временно–го ряда – для обеспечения сопоставимости числителя и знаменателя при расчете средних и относительных величин. Метод расчета среднего уровня ряда динамики зависит прежде всего от характера показателя, лежащего в основе ряда. Наиболее просто исчисляется средний уровень интервального ряда динамики абсолютных величин с равностоящими уровнями. Расчет производится по формуле простой средней арифметической:
где n – число фактических уровней за последовательные равные отрезки времени. Сложнее обстоит дело с исчислением среднего уровня моментного ряда динамики абсолютных вели–чин. Моментный показатель может изменяться почти непрерывно. Поэтому очевидно, что, чем более по–дробными и исчерпывающими данными о его изменении мы располагаем, тем более точно можно исчи–54б зависит от того, насколько подробны имеющиеся данные. Здесь возможны различные случаи. При наличии исчерпывающих данных об изменении моментного показателя его средний уровень исчисляется по формуле средней арифметической взвешенной для интервального ряда с разностоящими уровнями:
где t – число периодов времени, в течение которых уровень не изме–нялся. Если промежутки времени между соседними датами равны друг другу, т. е. когда мы имеем дело с равными (или примерно равными) интервалами между датами, тогда для моментального ряда с равностоящими уровнями расчет среднего уровня ряда производим по формуле средней хронологической:
Для моментального ряда с разностоящими уровнями расчет среднего уровня ряда производится по формуле:
Выше шла речь о среднем уровне рядов динами–ки абсолютных величин. Для рядов динамики средних и относительных величин средний уровень нужно исчислять исходя из содержания и смысла этих средних и относительных показателей.
49. Изучение основной тенденции развития в рядах динамики. Закономерности изменения явления во времени не проявляются в каждом конкретном уровне ряда. Это связано с действием на явления общих и случайных причин. Поэтому в статистике для выявления закономерности или тенденции развития явления используют следующие методы обработки рядов динамики: 1. Метод сглаживания путем укрупнения интервалов во времени. 2. Выравнивание рядов динамики методом скользящей средней. 3. Метод аналитичного выравнивания. Сущность приема укрепления интервалов сводится к следующему: I прием. Первоначальный ряд динамики преобразуется и заменяется другим рядом, в котором показатели относятся к большим по продолжительности периодам времени, т.е. интервал укрупнен. Этот прием используется только для интервальных рядов динамики. Укрупнение производится до тех пор, пока не будет выявлена четкая тенденция развития явления, а уровни ряда охватывать большие периоды времени. II прием. Метод скользящей средней заключается в следующем: формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня ряда на один уровень. По укрупненным интервалам определяем среднюю из уровней, входящих в каждый интервал. Недостатки: 1. Невозможность получения всех уровней для сглаженного ряда. Число уровней в сглаженном РД меньше, чем в исходном, на (к – 1), где к – число периодов в укрупненном интервале (5 – 1) = 4, т. е. на 4. 2. Произвольность выбора интервала для определения скользящей средней. III прием: Аналитическое выравнивание. При исчислении этого метода фактические уровни РД заменяются теоретическими, вычисленными на основе уравнения определенной кривой, отражающей общую тенденцию развития явления. Тенденцию развития социально-экономических явлений обычно изображают кривой, параболой, гиперболой и прямой линией. Если РД выравнивают по прямой, то уравнение прямой имеет следующий вид: где у – фактические уровни; уt – теоретическое значение уровня; t – периоды времени – фактор времени. «а» и «в» – параметры уравнения. 50. Экстраполяция и интерполяция в рядах динамики. Интерполяция применяется для определения величины промежуточных уровней на основе известных смежных уровней ряда. Метод интерполяции применяется на известном предположении характера изменения уровней ряда динамики, который основывается на количественных оценках абсолютных приростов или темпов роста. Если ряд динамики имеет примерно одинаковые цепные абсолютные приросты, то промежуточные неизвестные уровни ряда определяются по формуле: где Если ряд динамики имеет примерно одинаковые цепные темпы роста, то неизвестные промежуточные уровни ряда определяются по формуле: Экстраполяция – это определение неизвестных уровней динамического ряда, лежащих за его пределами, т. е. либо будущих уровней, либо уровней, предшествующих начальному. При экстраполяции исходят из предположения, что характер динамики, выявленный за определённый период времени, сохраняется и в будущем (или имеет место в прошлом). Метод экстраполяции применяют чаще всего при прогнозировании будущих значений экономических явлений и процессов. Если ряд динамики имеет примерно одинаковые цепные абсолютные приросты, то значения будущих уровней ряда определяются по формуле: где Если ряд динамики имеет примерно одинаковые цепные темпы роста, то значения будущих уровней ряда определяются по формуле:
51. Понятие об индексах, их значение. Слово “индекс” (лат. index) означает показатель, указатель, опись. Однако не всякий показатель является индексом. Объем товарооборота, средняя заработная плата, удельный вес того или иного товара, количество товарооборота, приходящееся на 1 кв. м площади торгового зала, и т. п. – все показатели, характеризующие хозяйственную деятельность. Однако эти показатели не являются индексами. Индексы – показатели особого рода. Прежде всего, это относительные величины, характеризующие динамику явления (выполнение плана или сравнение регионов по тем или иным экономическим показателям). От обычных относительных величин индексы отличает то, что они характеризуют отношение сложных явлений, складывающихся под влиянием различных причин. Индексы, как правило, не ограничиваются простым показом отношения, а выявляют роль и значение отдельных условий и составных частей данного сложного явления. Например, индекс цен показывает, как изменились цены на все товары или отдельную группу товаров, как отразилось это изменение на соотношении количества и цен отдельных товаров, как само изменение цен отразилось на товарообороте, покупательной способности рубля, степени удовлетворения покупательского спроса. Индекс применяется также для изучения роли факторов, оказывающих влияние на изменение данного явления. Так, с помощью взаимосвязи индексов можно определить, в какой мере увеличение объема продукции зависит от роста производительности труда и в какой мере – от увеличения численности рабочих. Таким образом, индекс характеризует изменение величины сложного экономического явления, состоящего из элементов, которые непосредственно нельзя суммировать, поэтому он является более сложным и многосторонним показателем, чем относительные или средние величины. Например, можно ли определить все изменения товарооборота в натуральном выражении? Нет, так как реализуемые товары имеют различные натуральные единицы измерения (крупа в килограммах, растительное масло в литрах, обувь в парах, ткани в метрах и т. д.). Следовательно, складывать объемы разнородных товаров для определения динамики товарооборота нельзя. Суммирование будет возможным только в тех случаях, когда все товары будут приведены к сопоставимому виду, что достигается путем индексных расчетов. Индексом показывается относительная величина, характеризующая изменение сложных экономических явлений во времени и в пространстве и в то же время уровень планового задания и степень выполнения плана. Элементами любого индекса являются: а) индексируемая величина; б) тип (форма) индекса; в) веса индекса; г) сроки исчисления. В зависимости от элемента (а) возможны индекс цен, индекс физического (натурального) объема продукции, индексы производительности труда и т. д. В зависимости от типа (б) различают индексы агрегатные и индексы средние, а среди последних, смотря по форме средней, – индексы средние арифметические, индексы средние гармонические, индексы средние геометрические и т. д. В зависимости от весов (в) различают индексы простые (невзвешенные) и индексы взвешенные, а среди последних – индексы с постоянными (неизменными) весами и индексы с переменными весами (в меру необходимости с течением времени пересматриваемыми). В зависимости от сроков исчисления (г) рассматривают индексы базисные (с постоянной, неизменной во времени базой) и индексы цепные.
52. Принципы построения индивидуальных индексов. Способы построения индексов зависят от содержания изучаемого явления, методологии расчета исходных статистических показателей и целей исследования. В каждом индексе выделяют 3 элемента: В каждом индексе выделяют 3 элемента: § индексируемый показатель — это показатель, соотношение уровней которого характеризует индекс § сравниваемый уровень — это тот уровень, который сравнивают с другим. § базисный уровень — это тот уровень, с которым производится сравнение. Для расчета индекса необходимо найти отношение сравниваемого уровня к базисному и выразить его в виде коэффициента, если база сравнения приравнивается к единице, или в процентах, если база сравнения принимается за 100%. Обычно расчеты индексов производятся в форме коэффициентов с точностью до третьего знака после запятой, т. е. до 0,001, в форме процентов — до десятых долей процента, т.е. до 0,1%. Для удобства построения индексов используется специальная символика: § i — символ индексируемого показателя — индекс, характеризующий изменение уровня элемента явления. § I — с подстрочным индексируемым показателем — для группы элементов или всей совокупности в целом. § q — количество проданных товаров или произведенной продукции в натуральном выражении § p — цена за единицу товара § z — себестоимость единицы продукции § w — производительность труда § T — отработанное время или численность работников § l — средняя заработная плата одного работника § 0 — базисный период § 1 — отчетный период Индивидуальный индекс цен определяется как отношение цены отдельного товара в отчетном периоде к цене его в базисном периоде, то есть по формуле: Индивидуальный индекс товарооборота характеризует изменение товарооборота по одному товару и строится как отношение товарооборота отчетного периода
Разница между числителем и знаменателем его покажет абсолютное изменение товарооборота в рублях за счет двух фактров: изменения количества проданного товара и изменения цены этого товара, то есть
53. Принципы построения сводных (агрегатных) индексов. Общие (сводные) индексы выражают сводные (обощающие) результаты совместного изменения всех единиц, образщих изучаемую совокупность. Могут рассчитываться в агрегатной и в средней формах. Сущность агрегатного индекса индекса в том, что несоизмеримые элементы индексного набора приводят к соизмеримому виду путём их взвешивания (умножения) на соизмерители веса и дальнейшего суммирования по всем элементам индексного набора. Соизмерители необходимы для перехода от натур-х измерителей разнородных ед-ц статист-ой совок-ти к однород-м показ-ям. Соизмерители остаются постоянными на одном уровне (текущ или базис-го периода). Таким образом, на величине агрег-го инд-са сказывается влияние только фактора, который определяет измен-е индексир-ой вел-ны. Например, агрегатные инд-сы: 1)цен: Ip=∑p1q1/∑p0q1 2)физ объёма прод-ии: Iq=∑q1p0/∑q0p0 3)стоимост-го объёма прод-и: Ipq=∑p1q1/∑p0q0 Разностью числителя и знаменателя формул определяется абсол-е изм-е стоимост-го объёма продукции как в целом, так и за счёт изучаемых факторов: - общее изм-ие стоимостного объёма: ∆pq=∑p1q1-∑p0q0 - изм-е стоим-го объёма за счёт цен: ∆pqp=∑p1q1-∑p0q1 - изм-е стоим-го объёма за счёт физ объёма: ∆pqq=∑q1p0-∑q0p0 Между агрегатными инд-ми сущ-ет та же взаимосвязь, что и между показателями. Т.е. т.к. pq=p*q, значит Ipq=Ip*Iq=∑p1q1/∑p0q1*∑q1p0/q0p0=∑p1q1/∑p0q0 Следует отметить, что при расчёте как индив-х так и общих индексов, разл-т инд-сы объёмных показ-лей, т.е. таких показ-лей размер которых предст-ен в виде абс-х величин, и кач-х показ-лей. Объёмные пок-ли – хар-т размеры совок-ти, либо в натур, либо в ден ед-цах изм-я. Кач показ-ли – это показ-ли, которые рассчитаны на основании операций с объёмными показ-ми. Величина кач показ-ля как правило представлена в расчёте на ед-цу совокупности. При построении агрегатных индексов возн-ет проблема выбора весов. Если в агрегатном факт-ом индексе переменной явл-ся кач-й признак в числовом выражении, т.е. признак полученный расчётным путём, то такие инд-сы берут на ур-не отч-го периода: Ip=∑p1q1/∑p0q1 (такой инд-с, где веса учит-ся на ур-не отч-го периода – индекс Пааше!) Если индексируется объёмный показ-ль, т.е. пок-ль, харак-щий объём продукции, числ-ть занятых, объём осн-х фондов. условные пост-ые веса берутся на ур-не базисного периода: Iq=∑q1p0/∑q0p0 (такой индекс, где веса взяты на уров-не базисного периода – индекс Ласпейреса). 54 Средний арифметический и гармонический индексы. Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов. Он должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая. Среднеарифметический индекс тождествен агрегатному, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного по формуле средней арифметической, будет равна агрегатному индексу. В тех случаях, когда не известны отдельные значения p1 и q1, а дано их произведение р1q1 – товарооборот отчетного периода и индивидуальные индексы цен ip=р1/q1, а сводный индекс должен быть вычислен с отчетными весами, применяется среднегармонический индекс цен. Причем индивидуальные индексы должны быть взвешены таким образом, чтобы среднегармонический индекс совпал с агрегатным. Из формулы ip=р1/р0 определим неизвестное р0 значение и, заменив в формуле агрегатного индекса цен (2.2) значение р0=р1/ip, получим среднегармонический индекс цен: Таким образом, весами при определении среднегармонического индекса себестоимости являются издержки производства текущего периода, а при расчете индекса цен стоимость продукции этого периода. Агрегатная форма индекса является основной определяющей формой. Но не всегда можно воспользоваться именно этой формой индекса. Например, если нет данных о количестве проданных товаров, то индекс физического объема по агрегатной формуле исчислить нельзя. Но его можно построить в форме средней величины из соответствующих индивидуальных индексов. Агрегатный индекс качественных показателей можно преобразовать в гармоническую форму индекса. Для преобразования воспользуемся агрегатным индексом цен (индекс Пааше):
Подставляем в знаменатель индекса вместо p0 равное ему выражение
Этот индекс является средним гармоническим взвешенным индексом цен, Аналогично, путем простых подстановок, можно получить средний гармонический индекс себестоимости В преобразованных индексах теперь уже числитель остается неизменным и слагаемое числителя появляется в знаменателе. Таким образом, средний гармонический индекс будет тождествен агрегатному в том случае, если весами обратных значений индивидуальных индексов будут взяты слагаемые числителя агрегатного индекса. Средний гармонический индекс цен находит широкое применение при расчете индексов розничных цен. Что же касается, например, индекса себестоимости, то он исчисляется, как правило, по агрегатной формуле, т.к. на предприятиях имеется количественный учет произведенной продукции.
55. Индексы фиксированного и переменного состава. Индексы структурных сдвигов. Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Например, индекс переменного состава себестоимости продукции одного и того же вида рассчитывается по формуле:
где I пс – индекс переменного состава.
Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае себестоимости), но и структуры совокупности (весов). Индекс постоянного (фиксированного) состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксированного состава определяется как агрегатный индекс. Так, индекс фиксированного состава себестоимости продукции рассчитывают по формуле:
где /фс – индекс фиксированного состава.
Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления. Индекс определяется по формуле (при изучении изменения среднего уровня себестоимости):
где /сс – индекс структурных сдвигов.
Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:
56. Выбор базы и весов индексов. Выбор базы сравнения и весов индексов – это два важнейших методологических вопроса построения систем индексов. Система индексов – ряд последовательно построенных индексов. В зависимости от базы сравнения системы индексов бывают: · базисные – это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, т.е. в знаменателе всех индексов находится индексируемая величина базисного периода. · цепные – это ряд индексов одного и того же явления, вычисленных с меняющейся от индекса к индексу базой сравнения. Базисные индексы дают более наглядную характеристику общей тенденции развития исследуемого явления, а цепные – четче отражают последовательность изменения уровней во времени. Примеры построения системы индивидуальных индексов: Системы базисных и цепных индексов могут быть построены для агрегатных индексов. а) цепные индексы стоимости: б) базисные индексы стоимости: При построении систем индексов можно использовать постоянные и переменные веса. Системой индексов с постоянными весами называется система сводных индексов одного и тог же явления, вычисленных с весами, не меняющимися при переходе от одного индекса к другому. Постоянные веса позволяют исключить влияние структуры на величину индекса. · Система базисных индексов физического объема с постоянными весами
· Система цепных индексов физического объема с постоянными весами
Система индексов с переменными весами представляет собой систему сводных индексов одного и того же явления, вычисленных с весами, последовательно меняющимися от одного индекса к другому. · Система базисных индексов цен с переменными весами
· Система цепных индексов цен с переменными весами
Системы агрегатных индексов обладают теми же свойствами, что и системы индивидуальных индексов.
57. Взаимосвязи индексов. Между важнейшими индексами существуют взаимосвязи, позволяющие на основе одних индексов получить другие. Зная, например, значение цепных индексов за какой-либо период времени, можно рассчитать базисные индексы. И наоборот, если известны базисные индексы, то путем деления одного из них на другой можно получить цепные индексы. Существующие взаимосвязи между важнейшими индексами позволяют выявить влияние различных факторов на изменение изучаемого явления, например связь между индексом стоимости продукции, физического объема продукции и цен (раздел 12.7). Другие индексы также связаны между собой. Так, индекс издержек производства – это произведение индекса себестоимости продукции и индекса физического объема продукции:
Izq = Iz ∙ Iq (12.42)
или
Отсюда если себестоимость увеличилась на 10%, а количество продукции снизилось на 8%, то индекс издержек на производство будет равен:
1,10 ∙ 0,92 = 1,012, или 101,2%.
Индекс затрат времени на производство продукции может быть получен в результате умножения индекса физического объема продукции и величины, обратной величине индекса трудоемкости, т.е. индекс производительности труда
или
При увеличении физического объема продукции в текущем периоде на 15% по сравнению с базисным производительность снизилась на 18%, поэтому индекс затрат времени на производство продукции будет равен:
1,15: 0,82 = 1,402, или 140,2%.
Существует важная взаимосвязь между индексами физического объема продукции и индексами производительности труда. Индекс производительности труда рассчитывается на основе следующей формулы:
т.е. представляет собой отношение средней выработки продукции (в сопоставимых ценах) в единицу времени (или на одного занятого) в текущем и базисном периодах. Индекс физического объема продукции равен произведению индекса производительности труда на индекс затрат рабочего времени (или численности занятых):
Таким образом, если численность рабочих возросла на 12%, а производительность труда – на 7%, то индекс физического объема продукции будет равен:
1,12 ∙ 1,07 = 1,20, или 120%.
Взаимосвязь между отдельными индексами может быть использована для выявления влияния отдельных факторов, оказывающих воздействие на изучаемое явление
|

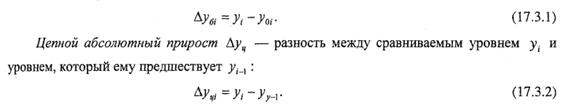 Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень показателя изучаемого периода ниже базисного. Между базисными и цепными абсолютными приростами имеется связь: сумма цепных абсолютных приростов ^Д^,,, равна базисному абсолютному приросту последнего периода ряда динамики A^g„:
Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень показателя изучаемого периода ниже базисного. Между базисными и цепными абсолютными приростами имеется связь: сумма цепных абсолютных приростов ^Д^,,, равна базисному абсолютному приросту последнего периода ряда динамики A^g„:
 Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Базисные темпы роста Tpg исчисляются делением сравниваемого уровня у, на уровень, принятый за постоянную базу сравнения уо,:
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Базисные темпы роста Tpg исчисляются делением сравниваемого уровня у, на уровень, принятый за постоянную базу сравнения уо,:
 Цепные темпы роста Трб исчисляются делением сравниваемого уровняв, на предыдущий уровень y0i:
Цепные темпы роста Трб исчисляются делением сравниваемого уровняв, на предыдущий уровень y0i:
 Если темп роста больше единицы (или 100%), то это указывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) указывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак. Базисный темп прироста Tg вычисляется делением сравниваемого базисного абсолютного прироста Ауд на уровень, принятый за постоянную базу сравнения уoi:
Если темп роста больше единицы (или 100%), то это указывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) указывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак. Базисный темп прироста Tg вычисляется делением сравниваемого базисного абсолютного прироста Ауд на уровень, принятый за постоянную базу сравнения уoi:
 Если уровни ряда динамики сокращаются, то соответствующие показатели темпа прироста будут со знаком минус, так как они характеризуют относительное уменьшение прироста уровня ряда динамики.
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала. Вычисляются темпы наращивания Тн делением цепных абсолютных приростов Av,
на уровень, принятый за постоянную базу сравнения уц,:
Если уровни ряда динамики сокращаются, то соответствующие показатели темпа прироста будут со знаком минус, так как они характеризуют относительное уменьшение прироста уровня ряда динамики.
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала. Вычисляются темпы наращивания Тн делением цепных абсолютных приростов Av,
на уровень, принятый за постоянную базу сравнения уц,:
 Из преобразований в формуле (17.3.10) следует, что темпы наращивания можно непосредственно определять по базисным темпам роста:
Из преобразований в формуле (17.3.10) следует, что темпы наращивания можно непосредственно определять по базисным темпам роста:
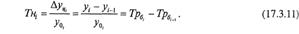 Формула (17.3.11) удобна для практики, так как статистическая информация о динамике социально-экономических явлений публикуется чаще всего в виде базисных рядов динамики.1
Формула (17.3.11) удобна для практики, так как статистическая информация о динамике социально-экономических явлений публикуется чаще всего в виде базисных рядов динамики.1
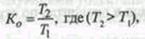 или
или 




 ,
,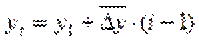
 - средний абсолютный прирост;
- средний абсолютный прирост;  - первый уровень ряда; i – порядковый номер уровня ряда.
- первый уровень ряда; i – порядковый номер уровня ряда. , где
, где  - средний темп роста.
- средний темп роста. ,
, - средний абсолютный прирост;
- средний абсолютный прирост;  - значение последнего уровня ряда; i – срок прогноза (i = 1,2,…n)
- значение последнего уровня ряда; i – срок прогноза (i = 1,2,…n)
 . Разность между числителем и знаменателем его покажет абсолютное изменение цены за единицу товара в рублях
. Разность между числителем и знаменателем его покажет абсолютное изменение цены за единицу товара в рублях  .
. к товарообороту базисного периода
к товарообороту базисного периода  , то есть по формуле:
, то есть по формуле: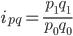


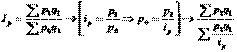 (2.8)
(2.8)
 В этом индексе числитель – величина известная, в знаменателе р0 можно заменить через индивидуальный индекс цен:
В этом индексе числитель – величина известная, в знаменателе р0 можно заменить через индивидуальный индекс цен: 
 .
. . Получаем следующую формулу индекса цен:
. Получаем следующую формулу индекса цен:
 и средний гармонический индекс трудоемкости
и средний гармонический индекс трудоемкости