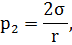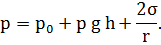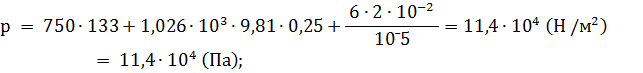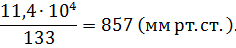Примеры решения задач. Бедренная кость собаки имеет длину 25 см и сечение 3 см2
ЗАДАЧА № 1 Бедренная кость собаки имеет длину 25 см и сечение 3 см2. Какая работа совершается при сжатии кости на 0,5 мм, если модуль упругости кости 20 ГПа?
Решение: Работа сжатия кости расходуется на увеличении ее потенциальной энергии, которая может быть вычислена по формуле:
где р – напряжение упруго сжатого тела; Е – модуль упругости; V=SL – объем тела. По этой же формуле может быть вычислена и работа сжатия кости. Следовательно,
Величина напряжения может быть вычислена по закону Гука:
Следовательно,
Подставляя это выражение в формулу работы, получим:
Проверим размерность полученной формулы.
Подставим числовые данные:
Ответ: работа сжатия кости равна 3 (Дж).
ЗАДАЧА №2 Определить радиус капилляра, в котором спирт. Плотность и КПН спирта приведены в таблицах.
Решение: Высота поднятия жидкости (смачивающейся) в капилляре определяется по формуле Жюрена:
Cчитая, что имеет место полное смачивание стенок капилляра спиртом, можно написать, что величина краевого угла
Проверим размерность полученной формулы:
Произведем вычисления:
Ответ: радиус капилляра равен 70 (мкм).
ЗАДАЧА № 3 В сосуде находится сыворотка крови, плотность которой 1026 кг/
Решение: Давление воздуха внутри пузырька равно сумме трех давлений: 1. Атмосферное давление Р0. 2.Давление собственного веса жидкости на глубине h, равное 3. Давление, создаваемое изогнутой поверхностью жидкости, которая в случае сферической поверхности определяется по формуле (формула Лапласа):
где r - радиус сферической поверхности. Таким образом, давление внутри пузырька равно:
Подставим в полученное выражение числовые данные:
Ответ: давление воздуха в пузырьке равно 114 кПа (857 мм рт.ст).
|

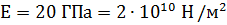
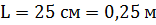
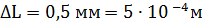
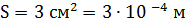
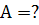


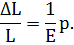
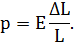
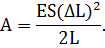
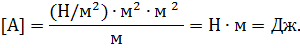
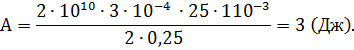
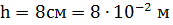
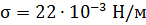


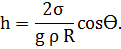
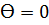 и соs
и соs 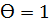 . Отсюда радиус капилляра
. Отсюда радиус капилляра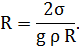

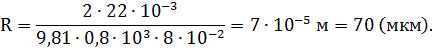
 и КПН которой равен
и КПН которой равен  Н/м. На глубине 25 см от поверхности жидкости образовался пузырек воздуха диаметром 10 мкм. Определить давление воздуха в пузырьке, если атмосферное давление равно 750 мм рт. столба.
Н/м. На глубине 25 см от поверхности жидкости образовался пузырек воздуха диаметром 10 мкм. Определить давление воздуха в пузырьке, если атмосферное давление равно 750 мм рт. столба.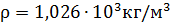
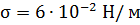
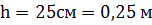
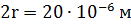
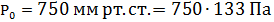
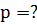
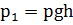 .
.