Примеры решения задач. В лабораторном помещении, находящемся в здании птичника, уровень интенсивности шума достигал 80 дБ
ЗАДАЧА № 1 В лабораторном помещении, находящемся в здании птичника, уровень интенсивности шума достигал 80 дБ. С целью уменьшения шума было решено обить стены лаборатории звукопоглощающим материалом, уменьшающим интенсивность звука в 1500 раз. Какой уровень интенсивности шума станет после этого в лаборатории?
Решение: Уровень интенсивности звука в децибелах определяется соотношением
где При изменении интенсивности звука изменение уровня интенсивности звука будет равно:
Отсюда Подставляя числовые значения, получим:
Ответ: уровень интенсивности шума 48,24 (дБ).
ЗАДАЧА № 2 На границу раздела между водой и воздухом падает плоская звуковая волна с интенсивностью
Решение: Интенсивность звука в воде будет равна интенсивности звука в воздухе, умноженной на коэффициент проникновения звука
где p и v – соответственно плотности среды и скорости звука в этой среде, а произведение Подставим числовые значения:
Так как число
Подставляя числа, получим:
Коэффициент проникновения
Интенсивность звука, прошедшего в воду, равна:
Ответ: интенсивность звука в воде 0,57
|
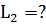
– условный нулевой уровень интенсивности звука (
).
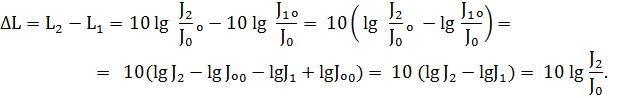
. Какова будет интенсивность звука, прошедшего в воду?
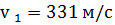
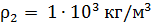
, где 
- коэффициент отражения на границе раздела двух сред, вычисляемый по формуле Рэлея:
есть акустическое сопротивление среды. Значения p и v для воздуха и воды приведены в условиях задачи.
мало по сравнению с единицей, воспользуемся правилами приближенных вычислений, приведенными на с. 7:
.
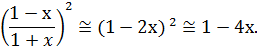
