Правила приближенных вычислений
Числовые значения физических величин, с которыми приходится иметь дело при решении задач, в большинстве случаев являются приближенными, причем степень приближения зависит как от точности приборов, которыми измерялась данная физическая величина, так и от тех требований, которые выдвигаются условиями задачи. Так, например, ускорение силы тяжести обычно принимается равным 9,81 м/с2. Однако более точные измерения этой величины могут дать значение 9,80665 м/с2. При решении же некоторых задач в целях упрощения расчетов можно принять значение этой величины равным 10 м/с2. Необходимо помнить, что точность конечного результата За сколько времени падающее тело достигнет скорости 50 м/с? В соответствии с законами свободного падения Чтобы избежать вычисления ненужных знаков, необходимо соблюдать правила действия над приближенными числами: 1. Следует правильно записывать приближенные числа. Так, например, числа 5,6; 5,60; 5,600 – отнюдь не одно и то же число. В первой записи указано, что верны лишь цифры целых и десятых долей. Во втором числе верны сотые доли, а в третьем – также и тысячные, и, следовательно, измерения, в которых получено это число, оказались наиболее точными из всех трех измерений. 2. При сложении и вычитании приближенных чисел в результате надо отбрасывать по правилам округления цифры тех разрядов справа, которых нет хотя бы в одном из слагаемых. Так, например:
Десятые доли отброшены, так как десятичные знаки первого слагаемого неизвестны. 3. При умножении и делении приближенных чисел в результате необходимо оставлять столько значащих цифр, сколько их имеется в числе с наименьшим количеством значащих цифр. Прочие цифры заменяются нулями или отбрасываются по правилам округления. Например:
4. При возведении в степень или извлечении корня в результате надо оставлять столько значащих цифр, сколько их в исходном числе, с которым производится действие. Например:
5. При вычислении сложных выражений следует применять указанные правила в соответствии с видом производимых действий. Например,
Числа 5,3 и 2,7 имеют наименьшее количество значащих цифр, а именно две. Поэтому результаты всех промежуточных вычислений должны округляться до трех знаков, оставляя, кроме двух достоверных, один сомнительный знак. Тогда предыдущее выражение можно будет записать так:
Произведя эти вычисления, округляем ответ до двух значащих цифр, т. е. до 4,7. 6. Табличные величины (число π, 7. В ряде случаев результаты измерений или табличные данные выражаются числами, близкими к единице, но заведомо не равными единице. При точных вычислениях такие числа округлять нельзя. Так, например, магнитная проницаемость платины равна 1,000360, показатель преломления воздуха равен 1,00029 и т. п. Вычисления с ними довольно громоздки. Поэтому при работе с такими числами следует пользоваться специальными правилами. Пусть число может быть выражено в виде
Рассмотрим применение этих правил на примерах:
Этими правилами следует широко пользоваться в приближенных вычислениях и при решении задач. Большую помощь при проведении вычислений оказывают микрокалькуляторы. Они полезны не только при решении задач по физике, но и в практической деятельности ветеринарного врача, а также в быту. Следует, однако, отметить, что микрокалькуляторы дают результаты с пятью, семью и с большим количеством знаков. Поэтому числа, даваемые микрокалькулятором, необходимо округлять в соответствии с вышеприведенными правилами. При вычислениях в ряде случаев удобно пользоваться таблицами 3 и 4, помещенными в конце указаний.
|

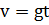 , a
, a  . Производя деление, можно получить, например, число 5,09684... секунд. Можно производить деление и дальше, но смысла это иметь не будет, так как вполне достаточно остановиться на числе 5,09, имеющем столько же значащих цифр, сколько их имеет исходное данное – 9,81. Излишнее количество знаков при вычислениях не только не приносит пользы, но является грубой ошибкой, так как говорит о том, что вычислитель не имеет представления о точности своих измерений и вычислений и бесполезно затрачивает свой труд и время.
. Производя деление, можно получить, например, число 5,09684... секунд. Можно производить деление и дальше, но смысла это иметь не будет, так как вполне достаточно остановиться на числе 5,09, имеющем столько же значащих цифр, сколько их имеет исходное данное – 9,81. Излишнее количество знаков при вычислениях не только не приносит пользы, но является грубой ошибкой, так как говорит о том, что вычислитель не имеет представления о точности своих измерений и вычислений и бесполезно затрачивает свой труд и время.
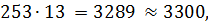
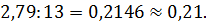



 , заряд электрона и т. п.) следует брать с таким количеством значащих цифр, которое равно количеству значащих цифр в наименее точном из данных по условиям задачи.
, заряд электрона и т. п.) следует брать с таким количеством значащих цифр, которое равно количеству значащих цифр в наименее точном из данных по условиям задачи. , где х – малое число. Тогда
, где х – малое число. Тогда .
. ,
,



 .
.


