Примеры решения задач. В дождевальной установке вода подается сначала по трубе диаметром 40 мм, а затем по трубе диаметром 24 мм
ЗАДАЧА №1 В дождевальной установке вода подается сначала по трубе диаметром 40 мм, а затем по трубе диаметром 24 мм. Статистические давления в широкой и узкой частях трубы равны соответственно 150 кПа и 60 кПа. Определить скорость течения воды в узкой части трубы.
Решение: Скорость движения жидкости в горизонтальной трубе переменного сечения (если не принимать во внимание трения) изменяется в соответствии с уравнением Бернулли:
Кроме того, как следует из уравнения неразрывности потока жидкости,
Подставим это значение v1 в уравнение Бернулли:
Отсюда: Следовательно, Проверим размерность полученного выражения. Член, стоящий в квадратных скобках, безразмерный, поэтому
Таким образом, размерность правой части полученного выражения совпадает с размерностью скорости. Подставим числовые значения заданных величин:
Ответ: скорость течения воды в узкой части трубы равна 14, 4 (м/с).
ЗАДАЧА № 2 В касторовое масло опустили стальной шарик диаметром 1 мм и определили, что расстояние в 5 см он прошел за 14,2с. Считая движение шарика равномерным, определить вязкость касторового масла, если его плотность равна
Решение: На шарик, движущийся в вязкой жидкости, действуют три силы: 1) сила тяжести (вниз)
2) выталкивающая, архимедова, сила (вверх)
2) cила трения, определяемая по закону Стокса (вверх)
При равномерном движении шарика алгебраическая сумма этих сил должна равняться нулю, т. е
После несложных преобразований получаем:
Поскольку скорость равномерного движения шарика
Проверим размерность полученного выражения:
Таким образом, размерность правой части полученного выражения совпадает с размерностью коэффициента внутреннего трения. Подставляем числовые значения:
Ответ: коэффициент вязкости касторового масла равен 1,07
ЗАДАЧА №3 Определить время протекания крови через капилляр вискозиметра, если вода протекает через него за 10 с. Объемы воды и крови одинаковы. Решение: Эта задача решается применением закона Гагена-Пуазейля, согласно которому объемный расход жидкости при ламинарном течении в трубе пропорционален четвертой степени радиуса трубы и градиенту давления и обратно пропорционален коэффициенту вязкости:
где r – радиус трубы; ∆р – градиент давления; L – длина трубы;
Из этой формулы следует, что объем жидкости, протекающий через сечения трубы за время t, равен (с учетом
Пусть через одну и ту же трубу за одно и то же время протекает одинаковое количество жидкостей, одна из которых – исследуемая, а другая – эталонная, т. е обладающая известным коэффициентом вязкости. Так как при этом V=Vэ, то, очевидно, можно написать:
После сокращения на одинаковые множители получим:
Отсюда время протекания исследуемой жидкости будет равно:
(в этих формулах мы обозначили индексом «э» величины, относящиеся к эталонной жидкости). Коэффициенты вязкости воды и крови соответственно равны: Произведем вычисления:
Ответ: кровь будет протекать через капилляр вискозиметра 12,6 (мин).
|




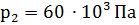

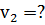

 , где
, где  и
и  - сечения трубы. Таким образом, неизвестная скорость
- сечения трубы. Таким образом, неизвестная скорость  может быть выражена через искомую скорость v2, т. е
может быть выражена через искомую скорость v2, т. е
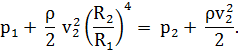

 .
.

 , а плотность стали 7860
, а плотность стали 7860  .
.





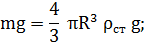
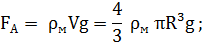
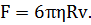







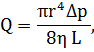
 – объемный расход жидкости, т. е объем жидкости, протекающий через сечения трубы в единицу времени;
– объемный расход жидкости, т. е объем жидкости, протекающий через сечения трубы в единицу времени;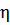 – динамический коэффициент вязкости.
– динамический коэффициент вязкости. где
где 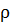 - плотность жидкости).
- плотность жидкости).
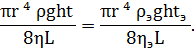
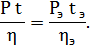

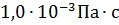 и
и  , плотности воды и крови соответственно равны:
, плотности воды и крови соответственно равны:  .
.



