Решение. Расширенная матрица системы имеет вид
Здесь
Расширенная матрица системы имеет вид
Выполним прямой ход метода Гаусса. Шаг 1. Для удобства вычислений поменяем местами первую и вторую строки:
Так как
Шаг 2. Так как
Получили систему уравнений, соответствующую последней матрице:
откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения Ответ: (3; -5; 2).
Контрольная работа №1
I. 1. Найти ранг матрицы системы; исследовать систему линейных уравнений на совместность: а) методом элементарных преобразований; б) методом окаймляющих миноров. 2.Решить систему линейных уравнений: а) по формулам Крамера; б) методом обратной матрицы; в) методом Гаусса. 3. Найти обратную матрицу: а) методом Гаусса б) сделать проверку
1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. II. Найти множество решений однородной системы трех линейных уравнений с четырьмя неизвестными. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. III. Вычислить определитель четвертого порядка: 1. 4. 7. 10. 13. 16. 19. 22. 25. 28. IV. Вычислить матрицу
|

 .
. .
. .
. , то умножая первую строку на (-2) и на (-1) и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную
, то умножая первую строку на (-2) и на (-1) и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную  из всех строк, начиная со второй:
из всех строк, начиная со второй: .
. , то умножим вторую строку на (-3/5) и прибавим к третьей, таки образом исключим переменную
, то умножим вторую строку на (-3/5) и прибавим к третьей, таки образом исключим переменную  из третьей строки:
из третьей строки: .
.
 ; из второго уравнения найдем
; из второго уравнения найдем  ; из первого уравнения
; из первого уравнения  .
. ;
; .
. 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 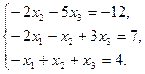
 24.
24. 
 26.
26. 
 28.
28. 
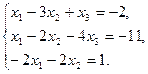 30.
30. 
 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 
 ; 2.
; 2.  ; 3.
; 3.  ;
; ; 5.
; 5.  ; 6.
; 6. 
 ; 8.
; 8.  ; 9.
; 9.  ;
; ; 11.
; 11.  ; 12.
; 12.  ;
; ; 14.
; 14.  ; 15.
; 15.  ;
; ; 17.
; 17.  ; 18.
; 18.  ;
; ; 20.
; 20.  ; 21.
; 21.  ;
; ; 23.
; 23.  ; 24.
; 24.  ;
;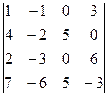 ; 26.
; 26.  ; 27.
; 27. 
 ; 29.
; 29.  ; 30.
; 30.  .
. , если:
, если: ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
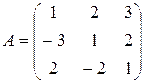 ,
,
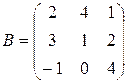 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
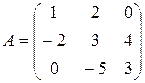 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
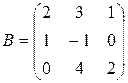 ;
;
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 .
.



