Глава 3. Правовое обеспечение социальной работы учреждений социального обслуживания
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору Векторы
Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости.
Пусть заданы два вектора Уравнение плоскости:
Уравнение плоскости по точке и вектору нормали.
A(x – x0) + B(y – y0) + C(z – z0) = 0.
Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор Таким образом, получаем уравнение плоскости
Теорема доказана. Уравнение плоскости в отрезках. Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D)
Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.
Уравнение плоскости в векторной форме.
a, b и g - углы, образованные этим вектором с осями х, у, z.
В координатах это уравнение имеет вид: xcosa + ycosb + zcosg - p = 0.
Расстояние от точки до плоскости.
Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.
Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой: A(x – x0) + B(y – y0) + C(z – z0) = 0.
Пример. Найти уравнение плоскости, проходящей через две точки P(2; 0; -1) и Q(1; -1; 3) перпендикулярно плоскости 3х + 2у – z + 5 = 0. Вектор нормали к плоскости 3х + 2у – z + 5 = 0 Получаем:
Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2 z – 3 = 0. Искомое уравнение плоскости имеет вид: A x + B y + C z + D = 0, вектор нормали к этой плоскости
Таким образом, вектор нормали Итого, получаем уравнение плоскости: 11 x - 7 y – 2 z – 21 = 0. Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость. Находим координаты вектора нормали 16 + 9 + 144 + D = 0 D = -169 Итого, получаем искомое уравнение: 4 x – 3 y + 12 z – 169 = 0
Пример. Даны координаты вершин пирамиды А1(1; 0; 3), A2(2; -1; 3), A3(2; 1; 1), A4(1; 2; 5). 1) Найти длину ребра А1А2.
2) Найти угол между ребрами А1А2 и А1А4.
Найти угол между ребром А1А4 и гранью А1А2А3. Сначала найдем вектор нормали к грани А1А2А3
Найдем угол между вектором нормали и вектором
Искомый угол g между вектором и плоскостью будет равен g = 900 - b.
3) Найти площадь грани А1А2А3.
4) Найти объем пирамиды.
5) Найти уравнение плоскости А1А2А3. Воспользуемся формулой уравнения плоскости, проходящей через три точки.
2x + 2y + 2z – 8 = 0 x + y + z – 4 = 0; При использовании компьютерной версии “ Курса высшей математики ” можно запустить программу, которая решит рассмотренный выше пример для любых координат вершин пирамиды. Для запуска программы дважды щелкните на значке: В открывшемся окне программы введите координаты вершин пирамиды и, нажимите Enter. Таким образом, поочередно могут быть получены все пункты решения. Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Глава 3. Правовое обеспечение социальной работы учреждений социального обслуживания
|

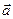 .
.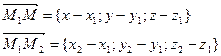 и вектор
и вектор 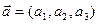 должны быть компланарны, т.е. (
должны быть компланарны, т.е. (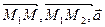 ) = 0
) = 0 Уравнение плоскости:
Уравнение плоскости: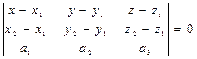
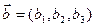 , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы
, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы 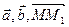 должны быть компланарны.
должны быть компланарны.
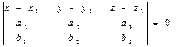
 Теорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали
Теорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали 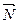 (A, B, C) имеет вид:
(A, B, C) имеет вид: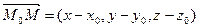 . Т.к. вектор
. Т.к. вектор 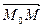 . Тогда скалярное произведение
. Тогда скалярное произведение 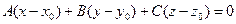
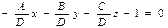 ,
, заменив
заменив 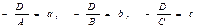 , получим уравнение плоскости в отрезках:
, получим уравнение плоскости в отрезках: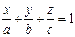

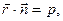 где
где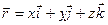 - радиус- вектор текущей точки М(х, у, z),
- радиус- вектор текущей точки М(х, у, z),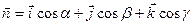 - единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат.
- единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат. p – длина этого перпендикуляра.
p – длина этого перпендикуляра. Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:
Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно: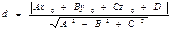
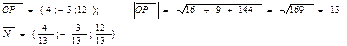
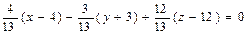
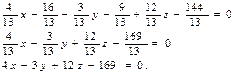
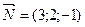 параллелен искомой плоскости.
параллелен искомой плоскости.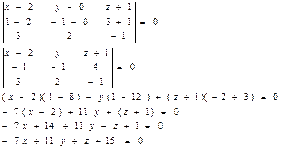
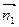 (A, B, C). Вектор
(A, B, C). Вектор  (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали
(1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали 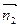 (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то
(1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то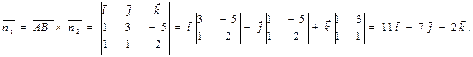
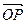 = (4, -3, 12). Искомое уравнение плоскости имеет вид: 4 x – 3 y + 12 z + D = 0. Для нахождения коэффициента D подставим в уравнение координаты точки Р:
= (4, -3, 12). Искомое уравнение плоскости имеет вид: 4 x – 3 y + 12 z + D = 0. Для нахождения коэффициента D подставим в уравнение координаты точки Р:
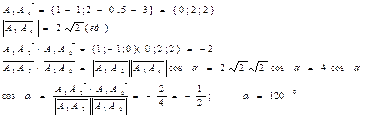
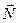 как векторное произведение векторов
как векторное произведение векторов 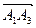 и
и 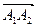 .
.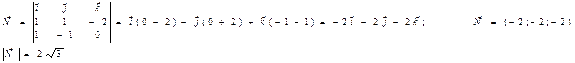
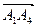 .
.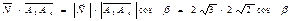
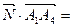 -4 – 4 = -8.
-4 – 4 = -8.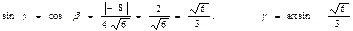
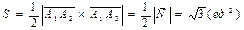
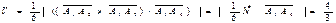 (ед3).
(ед3).