Реферат. 1. Физическая химия как наука
1 семестр 2015 / 2016 уч. год.
1. Физическая химия как наука. Основные разделы физической химии. Область исследования и задачи химической термодинамики. 2. Основные понятия. Термодинамическая система и окружающая среда. Классификация термодинамических систем по характеру взаимодействия с окружающей средой. Состояние системы и термодинамические параметры. Экстенсивные и интенсивные параметры, функции. Уравнения состояния. Термодинамические процессы и их классификация. Термодинамическое равновесие. 3. Основные законы термодинамики. Закон термического равновесия (нулевое начало термодинамики). Первое начало термодинамики. Теплота и работа как формы передачи энергии. Виды работы. Применения первого начала термодинамики к изохорическому, изобарическому, изотермическому и адиабатическому процессам в закрытой системе в отсутствие полезной работы. Внутренняя энергия и энтальпия как функции состояния, связь между ними. Физический смысл газовой постоянной. 4. Термохимия. Тепловой эффект реакции. Закон Гесса и условия его применимости. Применение закона Гесса к расчету тепловых эффектов реакций. Термохимические уравнения. Стандартный тепловой эффект реакции. Стандартная энтальпия образования. Следствия из закона Гесса. Стандартная теплота сгорания. 5. Теплоемкость (удельная, мольная). Мольная теплоемкость (изохорная и изобарная). Теплоемкость идеального газа. Соотношение между Cp и C v для идеального газа. Теплоемкость твердых тел. Правила Дюлонга и Пти; Неймана-Коппа. Закон Дебая. 6. Зависимость теплового эффекта реакции от температуры. Уравнение Кирхгофа и его анализ. Интегрирование уравнения Кирхгофа с учетом температурной зависимости теплоемкостей. 7. Второе начало термодинамики. Процессы самопроизвольные (естественные) и несамопроизвольные (искусственные). Различные формулировки II начала термодинамики и его математическое выражение. Применение II начала термодинамики к изолированным системам. Значение II начала термодинамики. Объединенное уравнение I и II начал термодинамики. Расчет изменения энтропии в различных процессах: изотермических (расширение–сжатие идеального газа, смешение идеальных газов, фазовые переходы I рода, химические реакции) и неизотермических (нагревание–охлаждение). Правило Трутона. 8. Связь энтропии с термодинамической вероятностью. Уравнение Больцмана, его физический смысл. Термодинамическая вероятность и направление самопроизвольных процессов в изолированной системе. 9. Постулат Планка (третье начало термодинамики). Остаточная энтропия. Расчет абсолютных энтропий веществ. 10. Применения объединенного уравнения I и II начал термодинамики к изотермическим процессам в закрытых системах. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых системах. Максимальная полезная работа. Характеристические функции. Фундаментальные уравнения для закрытых систем. Уравнения Гиббса–Гельмгольца. Фундаментальные термодинамические соотношения для открытых систем. Парциальные молярные величины. Химический потенциал идеального газа. 11. Термодинамика химического равновесия. Химическая переменная. Химическое равновесие, его условие и признаки. Термодинамический вывод закона действующих масс. Константы равновесия Kp, Kc и Kx, связь между ними. Уравнение изотермы химической реакции (изотермы Вант-Гоффа). Критерии направления химической реакции в изотермических условиях. Химическое равновесие с участием конденсированных веществ. Влияние температуры на химическое равновесие. Уравнение изобары химической реакции (изобары Вант-Гоффа), его вывод, анализ, интегрирование и применение. Принцип Ле Шателье. 12. Методы расчета изменения стандартной энергии Гиббса и константы равновесия химической реакции. 13. Химическое равновесие в неидеальных газовых смесях. Понятия фугитивности и коэффициента фугитивности. Химический потенциал компонента реальной газовой смеси. Закон действующих масс и уравнения изотермы и изобары химической реакции для неидеальной газовой системы. Методы расчета коэффициента фугитивности чистых газов. Билет ХТ-1-5-2015 1. Состояние термодинамической системы и термодинамические параметры. Экстенсивные и интенсивные параметры, функции. 2. Теплота сгорания вещества. Определите тепловой эффект реакции 3C2H2 = C6H6, используя справочные данные по теплотам сгорания. 3. Физический смысл энтропии. 7 моль водяного пара конденсируется при 100оС, далее вода охлаждается до 4оС. Как изменится энтропия воды? Средняя теплоемкость воды равна 4.2 Дж /(К∙г). Теплота испарения воды при нормальной температуре кипения равна 2258,1 Дж/г. 4. Фундаментальные уравнения для открытых систем. Химический потенциал и его смысл. Химический потенциал для идеального газа. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-6-2015 1. Первое начало термодинамики. Теплота и работа как формы передачи энергии. Виды работы. Внутренняя энергия и энтальпия как функции состояния, связь между ними. 2. Тепловой эффект реакции СО2 (г) + Н2 (г) = СО (г) + Н2О (г) в области 1100-1400 К равен 26,709 кДж/моль. Рассчитать константу равновесия Кp при 1200 К, если при 1100 К Кp = 4,235. 3. Энтропия. Вычислить изменение энтропии при нагревании 60 г монооксида азота от 298 К до 400 К. Зависимость теплоемкости: Cp = a + bT. 4. Критерии самопроизвольности процессов и условия равновесия в закрытых системах. Максимальная полезная работа. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-7-2015 1. Применения первого начала термодинамики к изохорическому, изобарическому и изотермическому процессам в закрытой системе в отсутствие полезной работы. 2. Теплота сгорания вещества. Определите тепловой эффект реакции C6H6 + 3H2 = C6H12, используя справочные данные по теплотам сгорания. 3. Энтропия. Вычислить изменение энтропии при расширении 80 г кислорода при T = const, если V1 = 60 л, V2 = 180 л. 4. Уравнение изотермы химической реакции (изотермы Вант-Гоффа). Критерии направления химической реакции в изотермических условиях. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-8-2015 1. Тепловой эффект реакции. Закон Гесса и условия его применимости. Применение закона Гесса к расчету тепловых эффектов реакций. 2. Теплота сгорания вещества. Определите тепловой эффект реакции 2CH4 = C2H2 + 3H2, используя справочные данные по теплотам сгорания. 3. Энтропия. Используя справ. данные, вычислите DS при нагревании 112 г азота от 298 К до 500 К. Зависимость теплоемкости: Cp = a + bT. 4. Химическое равновесие, его условие и признаки. Термодинамический вывод закона действующих масс. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-1-2015 1. Теплоемкость твердых тел. Правило Дюлонга и Пти. Правило аддитивности Неймана-Коппа. Закон Дебая. 2. Теплота сгорания вещества. Подберите коэффициенты в уравнении и определите тепловой эффект реакции CH3NO2 + H2 = CH3NH2 + H2O, используя справочные данные по теплотам сгорания. 3. Физический смысл энтропии. 3 моль водяного пара конденсируется при 100оС, вода охлаждается до 40оС. Как изменится энтропия воды? Средняя теплоемкость воды равна 1 Дж /(К∙г). Теплота испарения при нормальной температуре кипения равна 2258,1 Дж/г. 4. Химическое равновесие, его условие и признаки. Химическое равновесие с участием конденсированных веществ. Влияние температуры на химическое равновесие. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-2-2015 1. Зависимость теплового эффекта реакции от температуры. Уравнение Кирхгофа и его анализ. Интегрирование уравнения Кирхгофа с учетом температурной зависимости теплоемкостей. 2. Теплота сгорания вещества. Определите тепловой эффект реакции 3C2H2 + 3H2 = C6H12, используя справочные данные по теплотам сгорания. 3. Третий закон термодинамики. Как рассчитать абсолютную энтропию газа. Пользуясь законом Дебая найдите энтропию твердого хлора при 10 К, если известно значение Ср = 3,72 Дж/(моль К) при 15 К. 4. Вывод и анализ уравнения изотермы химической реакции (изотермы Вант-Гоффа). ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-3-2015 1. Различные формулировки II начала термодинамики и его математическое выражение. Значение II начала термодинамики. 2. Стандартная энтальпия образования. Расчет энтальпии реакции по энтальпиям химических связей. Определите стандартную энтальпию образования н-бутана, если энергии связей С-С и С-Н равны 351,46 и 411,22 кДж/моль. Теплота сублимации углерода 723,83 кДж/моль, энергия диссоциации водорода 430,95 кДж/моль. 3. Энтропия. 1 моль толуола испаряется при 111оС (т. кип.). Рассчитайте изменение энтропии. Теплота испарения 361,9 Дж/г. Сравните результаты расчета с расчетом по правилу Трутона. 4. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых системах. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-4-2015 1. Связь энтропии с термодинамической вероятностью. Уравнение Больцмана, его физический смысл. 2. Тепловой эффект реакции N2 (г) + О2 (г) = 2NО (г) в области 1700-2700 К равен 182,09 кДж/моль. Рассчитать константу равновесия Кp при 1800 К, если при 2200 К Кp= 1,1∙10-4. 3. Как рассчитать абсолютную энтропию газа. Вычислить изменение энтропии при нагревании 224 г азота от 298 К до 500 К. Зависимость теплоемкости: Cp = a + bT. 4. Применения объединенного уравнения I и II начал термодинамики к изотермическим процессам в закрытых системах. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-11-2015 1. Химический потенциал газа, изотермическая зависимость от давления. Стандартные состояния. 2. Подтвердите расчетом возможность протекания реакции в закрытой и изолированной системе, используя справочные данные: C2H4 + H2O = C2H5OH. 3. Энтропия. Используя справочные данные по Ср, вычислите изменение энтропии 3 моль азота при нагревании от 298 до 400 К с последующим изотермическим расширением в 2 раза. 4. Уравнение изотермы химической реакции (изотермы Вант-Гоффа). Критерии направления химической реакции в изотермических условиях. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-12-2015 1. Теплоемкость газов. Вклад различных видов движения молекул (одно- и двухатомных) во внутреннюю энергию и теплоемкость идеального газа. 2. Подтвердите расчетом возможность протекания реакции в закрытой и изолированной системе, используя справочные данные: C2H2 + H2O = CH3CHO. 3. Физический смысл энтропии. 5 моль водяного пара конденсируется при 100оС, вода охлаждается до 30оС. Как изменится энтропия воды? Средняя теплоемкость воды равна 4,2 Дж/(К∙г). Теплота испарения при нормальной температуре кипения равна 2258,1 Дж/г. 4. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых системах. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-9-2015 1. Химическое равновесие, его условие и признаки. Термодинамический вывод закона действующих масс. 2. Подтвердите расчетом возможность протекания реакции в закрытой и изолированной системе, используя справочные данные: C2H4 + HCl = C2H5Cl. 3. Третий закон термодинамики и абсолютная энтропия. Что такое So. Пользуясь законом Дебая найдите энтропию твердого аргона при 15 К, если известно значение Ср при 12 К. 4. Напишите уравнения Массье – полные дифференциалы термодинами-ческих потенциалов, а также формулы, связывающие эти потенциалы. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-10-2015 1. Основные определения термодинамики: теплота, работа, внутренняя энергия. 1-й закон термодинамики. 2. Подтвердите расчетом возможность протекания реакции в закрытой и изолированной системе, используя справочные данные: C6H6 + Cl2 = C6H5Cl + HCl. 3. Энтропия. Вычислить изменение энтропии при разделении 58 г воздуха при 0оС на компоненты. Состав воздуха: азот – 78 объем. %, кислород – 21 %, аргон – 1 %. 4. Термодинамика химического равновесия. Химическая переменная. Химическое равновесие, его условие и признаки. Термодинамический вывод закона действующих масс. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-15-2015 1. Теплоемкость газов. Вклад различных видов движения молекул во внутреннюю энергию и теплоемкость идеального газа. 2. Подтвердите расчетом возможность протекания реакции в закрытой и изолированной системе, используя справочные данные: C6H6 + F2 = C6H5F + HF. 3. Третий закон термодинамики и абсолютная энтропия. Как рассчитать абсолютную энтропию газа. Выведите общую формулу для расчета энтропии азота при 298 К. 4. Уравнение изобары химической реакции (изобары Вант-Гоффа), его вывод, анализ, интегрирование и применение. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-13-2015 1. Внутренняя энергия и энтальпия как функции состояния, связь между ними. Физический смысл газовой постоянной. 2. Подберите коэффициенты и подтвердите расчетом возможность протекания реакции в закрытой и изолированной системе, используя справочные данные: C6H5NO2 + H2 = C6H5NH2 + H2O. 3. Третий закон термодинамики и абсолютная энтропия. Как рассчитать абсолютную энтропию газа. Выведите общую формулу для расчета энтропии хлора при 298 К. 4. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых и изолированных системах. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-14-2015 1. Основные определения термодинамики: теплота, работа, внутренняя энергия. 1-й закон термодинамики. 2. Определите тепловой эффект реакции при 400 К: C2H4 + H2 = C2H6, используя справочные данные. Для расчета использовать среднюю теплоемкость. 3. Энтропия. Как рассчитать абсолютную энтропию газа. Вычислить изменение энтропии при разделении 58 г воздуха при 0оС на компоненты. Состав воздуха: азот – 78 объем. %, кислород – 21 %, аргон – 1 %. 4. Уравнение изотермы химической реакции (изотермы Вант-Гоффа). ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-16-2015 1. Термодинамическая вероятность и энтропия. Формула Больцмана. 2. Определите тепловой эффект реакции при 450 К: C6H6 + 3H2 = C6H12, используя справочные данные. Для расчета использовать среднюю теплоемкость. 3. Энтропия. Как рассчитать абсолютную энтропию газа. Вычислить изменение энтропии при разделении 116 г воздуха при 0оС на компоненты. Состав воздуха: азот – 78 объем. %, кислород – 21 %, аргон – 1 %. 4. Термодинамика химического равновесия. Химическая переменная. Химическое равновесие, его условие и признаки. Термодинамический вывод закона действующих масс. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-18-2015 1. Константы равновесия Kp и Kx, связь между ними. 2. Подберите коэффициенты в уравнении реакции и определите тепловой эффект реакции при 800 К: CH4 = H2 + C2H2, используя справочные данные (Cp = a + bT). 3. Третий закон термодинамики и абсолютная энтропия. Как рассчитать абсолютную энтропию газа. Выведите общую формулу для расчета энтропии азота при 298 К. Что такое So и как она учитывается при обычных расчетах. 4. Уравнение изобары химической реакции (изобары Вант-Гоффа), его вывод, анализ, интегрирование и применение. Принцип Ле Шателье. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-19-2015 1. Теплоёмкость газов. Уравнение Майера. 2. Уравнение Кирхгофа. Вывод и интегрирование с использованием зависимости Ср = a + bТ. Вычислить DrHо реакции N2O4 (ж) = 2NO2.(г) при 260 К. Использовать справочные данные. 3. Третий закон термодинамики и абсолютная энтропия. Как рассчитать абсолютную энтропию газа. Выведите общую формулу для расчета энтропии кислорода при 298 К. Что такое So и как она учитывается при обычных расчетах. 4. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых и изолированных системах. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-17-2015 1. Теплоемкость газов. Вклад различных видов движения молекул (одно- и двухатомных) во внутреннюю энергию и теплоемкость идеального газа. 2. Уравнение Кирхгофа. Вывод и интегрирование с использованием зависимости Ср = a + bТ. Используя справочные данные, вычислите DrHо реакции СO + H2O = HCOOH при 500 К. 3. Физический смысл энтропии. 18 г водяного пара конденсируется при 100оС, вода охлаждается до 0оС и кристаллизуется. Как изменится энтропия воды? Средняя теплоемкость воды равна 4,2 Дж /(К∙г). Теплота испарения при нормальной температуре кипения равна 2258,1 Дж/г, теплота плавления равна 333,5 Дж/г. 4. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых системах. Максимальная полезная работа. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-20-2015 1. Мольная теплоемкость (изохорная и изобарная). Соотношение между Cp и C v для идеального газа. 2. Уравнение Кирхгофа. Вывод и интегрирование с использованием зависимости Ср = a + bТ. Подберите коэффициенты в уравнении реакции и вычислите DrHо реакции CH4 = H2 + C2H2 при 700 К. Использовать справочные данные. 3. Физический смысл энтропии. 1 моль водяного пара конденсируется при 100оС, вода охлаждается до 0оС и кристаллизуется. Как изменится энтропия воды? Средняя теплоемкость воды равна 4,2 Дж /(К∙г). Теплота испарения при нормальной температуре кипения равна 2258,1 Дж/г, теплота плавления равна 333,5 Дж/г. 4. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых и изолированных системах. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-21-2015 1. Зависимость энергии Гиббса от температуры. Уравнение Гиббса-Гельмгольца. 2. Найдите теплоту образования AgCl из простых веществ при 500оС и p = const, если теплота образования при 298 К равна -126,78 кДж/моль. Теплоемкости можно принять постоянными и равными для серебра, хлора, хлорида серебра: 25,44; 33,93; 50,79 Дж/(моль∙К) соответственно. 3. Энтропия. Как рассчитать абсолютную энтропию газа. Определите изменение энтропии при смешении 800 г льда, взятого при температуре плавления, с 500 г водяного пара, взятого при нормальной температуре кипения. Что получится и при каких условиях? Средняя теплоемкость воды равна 4,2 Дж /(К∙г). Теплота испарения при нормальной температуре кипения равна 2258,1 Дж/г, теплота плавления равна 333,5 Дж/г. 4. Напишите уравнения Массье – полные дифференциалы термодинами-ческих потенциалов, а также формулы, связывающие эти потенциалы. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-22-2015 1. Константы равновесия Kp и Kс, связь между ними. 2. Стандартная теплота образования вещества. Напишите реакцию образования нитробензола, тепловой эффект которой отвечает стандартной теплоте образования жидкого нитробензола. 3. Третий закон термодинамики и абсолютная энтропия. Как рассчитать абсолютную энтропию газа. Выведите общую формулу для расчета энтропии аргона при 298 К. 4. Фундаментальные уравнения для открытых систем. Химический потенциал и его смысл. Зависимость химического потенциала идеального газа. Парциальные молярные величины. -------------------------------------------------------------------------- Билет ХТ-1-23-2015 1. Теплоемкость твердых тел. Правило Дюлонга и Пти. Правило аддитивности Неймана-Коппа. Закон Дебая. 2. Используя закон Гесса, рассчитайте теплоту сгорания циклогексана, если стандартная теплота образования его равна -156,23 кДж/моль, а теплоты образования воды и углекислого газа соответственно равны: -285,83 кДж/моль и -393,51 кДж/моль. 3. Используя справочные данные, определите константу равновесия при постоянном давлении (Кр) при 125oС для реакции: С6H6 (г) + 4Н2 (г) = С6H14 (г) 4. Энергия Гельмгольца и энергия Гиббса. Критерии самопроизвольности процессов и условия равновесия в закрытых и изолированных системах. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-24-2015 1. Термодинамическая вероятность и энтропия. Формула Больцмана. 2. Используя закон Гесса, рассчитайте теплоту сгорания н-гептана, если стандартная теплота образования его равна -198,82 кДж/моль, а теплоты образования воды и углекислого газа соответственно равны: -285,83 кДж/моль и -393,51 кДж/моль. 3. Используя справочные данные, определите константу равновесия при постоянном давлении (Кр) при 225oС для реакции: С6H6 (г) + 3Н2 (г) = С6H12 (г) 4. Характеристические функции. Фундаментальные уравнения для закрытых систем. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-25-2015 1. Энергия Гельмгольца: выражение, свойства, связь с максимальной полезной работой. Критерии самопроизвольности процессов и условия равновесия в закрытых системах. 2. Используя закон Гесса, рассчитайте теплоту сгорания изопропилового спирта, если стандартная теплота образования его равна -318,70 кДж/моль, а теплоты образования воды и углекислого газа соответственно равны: -285,83 кДж/моль и -393,51 кДж/моль. 3. Используя справочные данные, определите константу равновесия при постоянном давлении (Кр) при 200oС для реакции: С2H2 (г) + 2 Н2 (г) = С2H6 (г) 4. Напишите уравнения Массье – полные дифференциалы термодинами-ческих потенциалов, а также формулы, связывающие эти потенциалы. -----------------------------------------------------------------------------------------------------------------
Билет ХТ-1-26-2015 1. Энергия Гиббса: выражение, свойства, связь с максимальной полезной работой. Критерии самопроизвольности процессов и условия равновесия в закрытых системах. 2. Используя закон Гесса, рассчитайте теплоту сгорания пропилового спирта, если стандартная теплота образования его равна -304,55 кДж/моль, а теплоты образования воды и углекислого газа соответственно равны: -285,83 кДж/моль и -393,51 кДж/моль. 3. Энтропия. Используя справочные данные по Ср, вычислите изменение энтропии 2 моль азота при нагревании от 298 до 450 К с последующим расширением в 2 раза. 4. Константы равновесия Kp, Kc и Kx, связь между ними. ------------------------------------------------------------------------------------------------------- Билет ХТ-1-27-2015 1. Химическое равновесие, его условие и признаки. Термодинамический вывод закона действующих масс. 2. Используя закон Гесса, рассчитайте теплоту сгорания циклогексана, если стандартная теплота образования его равна -156,23 кДж/моль, а теплоты образования воды и углекислого газа соответственно равны: -285,83 кДж/моль и -393,51 кДж/моль. 3. Используя справочные данные, определите константу равновесия при постоянном давлении (Кр) при 55oС для реакции: СO (г) + Н2 (г) = С (гр.) + H2O (ж.) 4. Напишите уравнения Массье – полные дифференциалы термодинами-ческих потенциалов, а также формулы, связывающие эти потенциалы. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-28-2015 1. Напишите уравнения Массье – полные дифференциалы термодинамических потенциалов, а также формулы, связывающие эти потенциалы. 2. Используя закон Гесса, рассчитайте теплоту сгорания н-гексана, если стандартная теплота образования его равна -156,23 кДж/моль, а теплоты образования воды и углекислого газа соответственно равны: -285,83 кДж/моль и -393,51 кДж/моль. 3. Энтропия. Как рассчитать абсолютную энтропию газа. Используя справочные данные по Ср, вычислите изменение энтропии 2 моль кислорода при нагревании от 298 до 350 К с последующим расширением в 3 раза. 4. Константы равновесия Kp, Kc и Kx, связь между ними. ----------------------------------------------------------------------------------------------------------------- Билет ХТ-1-29-2015 1. Закон Кирхгофа и его интегрирование. Расчёты теплот реакций при разных температурах с использованием справочных таблиц. 2. Используя справочные данные определите константу равновесия при постоянном давлении (Кр) при 125oС для реакции: СO (г) + 3Н2 (г) = СН4 (г) + H2O (г) 3. Энтропия. Как рассчитать абсолютную энтропию газа. Вычислить изменение энтропии при разделении 58 г воздуха при 0оС на компоненты. Состав воздуха: азот – 78 объем. %, кислород – 21 %, аргон – 1 %. 4. Константы равновесия Kp, Kc и Kx, связь между ними. -----------------------------------------------------------------------------------------------------------------
Билет ХТ-1-30-2015 1. Соотношение между тепловыми эффектами при постоянном давлении и объеме. Теплоемкость. Уравнение Майера. 2. Используя справочные данные определите константу равновесия при постоянном давлении (Кр) при 25oС для реакции: С2Н2 (г) + H2O (г) = СН3СНО (г) 3. Стандартная энтальпия образования. Расчет энтальпии реакции по энтальпиям химических связей. Определите стандартную энтальпию образования н-гексана, если энергии связей С-С и С-Н равны 351,46 и 411,22 кДж/моль. Теплота сублимации углерода 723,83 кДж/моль, энергия диссоциации водорода 430,95 кДж/моль.
Реферат по учебной дисциплине: «Статистика» на тему: «Статистическое изучение корреляционной взаимосвязи явлений: понятие, виды, формы выражения тесноты связи» .
Выполнила: студентка 2-го курса группы МГБ-233-о Васильева Анастасия Николаевна Проверила: Рощина Юлия Викторовна
Симферополь 2015 Изучение действительности показывает, что изменение изучаемого признака находитсяв тесной взаимосвязи с другими признаками. При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обуславливающих изменения других признаков – они называются факторными признаками (Х). Признаки, которые являются результатом влияния этих факторных признаков, называются результативными признаками (У). Например: рассматривая зависимость между производительностью труда и квалификацией рабочих, уровень производительности труда является результативным признаком, а квалификация рабочих факторным, т.к. её повышение ведет к росту производительности труда. Различают два основных вида связей между явлениями. - функциональные связи характеризуются полнымсоответствием между изменением факторного и результативного признака (каждому значению признака – фактора соответствует вполне определенные значения результативного признака) y =f(x). Примером функциональной связи является зависимость длины окружности (L) от радиуса (r). L = 2Пr. - корреляционные связи, при которых между изменением факторного и результативного признаков нет полного соответствия, воздействия отдельных факторов проявляется лишь в среднем при массовомнаблюдении, фактических данных. В простейшем случае применения корреляционной зависимости величина результативного признака рассматривается как следствие изменения только одного фактора (например: рост квалификации рабочих рассматривается как причина роста производительности труда). Однако выделенный в данном примере в качестве основного признак – фактор не является единственной причиной изменения результативного признака, а на ряду с ним на величину результативного признака влияет множество других причин (в частности на производительность труда влияет уровень энерговооруженности, механизации и автоматизации производства). При наличии корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. Объяснения этому – сложность взаимосвязей между анализируемыми факторами, взаимодействие которых влияют неучтенные, случайные величины. Поэтому связь появляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента (х -признака фактора). Соответствует случайно распределенные в некотором интервале значения функции (у – признака результата). Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что удобрения участвуют в формировании урожая, для конкретного поля участии одного и того же количества удобрений вызовет разный прирост урожайности, так как во взаимодействии находится ещё целый ряд факторов (погода, состояние почвы и т. д.), которые формируют урожай. Однако в среднем такая связь наблюдается увеличение массы внесенных, удобрений ведет к росту урожайности. Виды взаимосвязей: a) По направлению связи делятся на: б) По степени тесноты:
в) По аналитическому выражению: Задачи статистики в изучении связей между явлениями заключается в следующем: 1. количественная оценка наличия и направления связи; 2. характеристика формы влияния одних факторов на другие (изменение степени тесноты корреляционной связи); 3. нахождение аналитического выражения связи (построение уравнений регрессии или корреляционно-регрессионных моделей); 4. оценка соответствия полученных моделей и их практическое использование.
13.2. Методы выявления наличия корреляционной связи между двумя признаками Для ответа на вопрос о наличии или отсутствии корреляционной связи используется ряд методов: - параллельное сопоставление рядов значений результативного и факторного признаков, является простейшим приёмом. Значения факторного признака располагаются в возрастающем порядке, а затем прослеживают направление изменения величины результативного признака; Однако наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, затрудняет восприятие таких параллельных рядов. В таких случаях для установления связи – пользуются статистическими таблицами – корреляционными и групповыми. Построение корреляционной таблицыначинают с группировки значений факторного и результативного признаков. При этом факторный признак (х), как правило, имеет конкретные значения и располагается в строках; а результативный признак (y) представлен в виде интервалов и располагается в столбцах таблицы. Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту построения данного сочетания значений Х и Y. Такая корреляционная таблица уже при общем знакомстве даёт возможность: - определить наличие или отсутствие связи; - выяснить её направление. Если частоты в корреляционной таблице расположены по диагонали из левого верхнего угла в правый нижний (т.е. большим значениям фактора соответствуют большие значения результата), то можно предположить наличие прямой корреляционной зависимости между признаками. Если же частоты располагаются с правого верхнего угла к левому нижнему, то предполагают наличие обратной связи. Построение групповой таблицы также начинают с группировки. По каждой группе вычисляют средние значения результативного признака, и дальше происходит сопоставление полученных данных. - Графический метод применяется для: · Предварительного выявления наличия или отсутствия связи; · Определения характера и формы связи. Используя данные об индивидуальных значениях признака-фактора и соответствующих значениях результативного признака, можно построить в прямоугольных осях точечный график, который называется поле корреляции. Определив среднее значение точек, можно построить линию, которая является эмпирической линией связи. Если эмпирическая линия связи приближается к прямой линии связи, то возможно наличие прямолинейной линии корреляционной связи между признаками. Если к какой-либо кривой, то возможна криволинейная корреляционная связь.
13.3. Измерение степени тесноты корреляционной связи между двумя признаками Понятно, что одни факторы влияют сильнее, другие слабее на результативный признак. Характеристика силы воздействия одних факторов на другие даётся при помощи показателей степени тесноты корреляционной связи между двумя признаками, к ним относятся: · Коэффициент корреляции знаков; · Линейный коэффициент корреляции; · Коэффициент корреляции рангов
а) Коэффициент корреляции знаков
б) Линейный коэффициент корреляции является более совершенным показателем степени тесноты связи. При расчёте этого показателя учитываются не только знаки отклонений, но и сами величины таких отклонений.
Есть много вариантов этой формулы. Много учёных занималось вопросами корреляции и в целом стохастических зависимостей (проявляется в массе случаев). Множественная корреляция. Коэффициент множественной корреляции:
0< в) Коэффициент корреляции рангов (коэффициент связи качественных признаков) Позволяет измерить тесноту связи между качественными признаками, которые не поддаются выражению числом. Каждой единице совокуп
|


 -
- 


 , где
, где - число совпадений знаков отклонения индивидуальных величин от средней факторного и результативного признаков;
- число совпадений знаков отклонения индивидуальных величин от средней факторного и результативного признаков; - число несовпадений знаков отклонений.
- число несовпадений знаков отклонений.
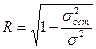 , где
, где - общая дисперсия фактических данных результативного признака, т.е. дисперсия y.
- общая дисперсия фактических данных результативного признака, т.е. дисперсия y. - остаточная дисперсия, характеризующая вариацию y за счёт факторов не включённых в уравнение регрессии.
- остаточная дисперсия, характеризующая вариацию y за счёт факторов не включённых в уравнение регрессии. - отражает тесноту связи между вариацией зависимой переменной и вариациями всех включённых в анализ независимых переменных
- отражает тесноту связи между вариацией зависимой переменной и вариациями всех включённых в анализ независимых переменных


