Порядок выполнения лабораторной работы в пакете Statistica
Порядок выполнения лабораторной работы рассмотрен на примере, в котором целью исследования является выявление взаимосвязей между показателями, характеризующими социально-демографическое положение муниципальных образований Оренбургской области. Объектом исследования выступают города и районы Оренбургской области, предметом исследования – социально-демографическое положение региона, характеризующееся следующими показателями:
Фрагмент таблицы с исходными данными в пакете Statistica 7.0 представлен на рисунке 3.1.
Рисунок 3.1 – Фрагмент исходных данных для анализа в пакете Statistica
Точечное оценивание параметров многомерного нормально распределенного вектора признаков сводится к оценке вектора математических ожиданий и ковариационной матрицы в виде вектора средних значений и выборочной ковариационной матрицы. Так, воспользовавшись пунктом меню «Statistics», подпунктами «Basic Statistics/Tables», «Descriptive statistics», получим таблицу, представленную на рисунке 3.2, в которой содержатся значения выборочных средних, дисперсий и средних квадратических отклонений для каждого признака.
Рисунок 3.2 – Результаты расчета средних значений признаков
Для получения выборочной ковариационной матрицы воспользуемся пакетом Excel, надстройкой «Пакет анализа». Необходимо ввести исходные данные в первые пять столбцов таблицы, затем выбрать пункт основного меню «Данные», подпункты «Анализ данных», «Ковариация». Вид экрана представлен на рисунке 3.3.
Рисунок 3.3 – Выбор пунктов меню в пакете Excel для получения оценки ковариационной матрицы
Далее необходимо заполнить появившуюся на экране форму «Ковариация». В поле «Входной интервал» указываются ячейки с исходными данными, в поле «Интервал вывода» указывается ячейка, с которой начнется вывод результатов. «Метки в первой строке» – флажок, который указывает, содержит ли первая строка названия столбцов или нет. Вид заполненной формы представлен на рисунке 3.4.
Рисунок 3.4 – Образец заполнения формы «Ковариация» в пакете Excel
После нажатия кнопки «ОК»на листе с исходными данными появятся результаты, представленные на рисунке 3.5.
Рисунок 3.5 – Результаты расчета выборочной ковариационной матрицы в пакете Excel
Таким образом, получены точечные оценки параметров многомерного нормально распределенного вектора признаков:
Анализируя вектор средних значений признаков, можно сделать следующие выводы: - общий коэффициент рождаемости в среднем по Оренбургской области составил 16,42‰; - среднее значение коэффициента брачности равно 9,29‰; - в среднем на территории Оренбургской области проживает 9,26% казахского населения; - средний по региону удельный вес населения, проживающего в коммунальных квартирах, составил 0,51%; - удельный вес женщин с одним ребенком в среднем по Оренбургской области равен 20,37% к общему числу женщин с детьми. Выборочные значения ковариаций позволяют сформулировать предположения о направлении связи между показателями, так, например, есть основания предполагать, что: - прямая зависимость существует между общим коэффициентом рождаемости ( - обратная зависимость наблюдается, например, между общим коэффициентом рождаемости ( Для расчета выборочных значений коэффициентов корреляции для каждой пары признаков необходимо выбрать пункты меню «Statistics», «Basic Statistics/Tables» (рисунок 3.6). В появившейся на экране форме (рисунок 3.7) необходимо выбрать пункт «Correlation matrices» и нажать кнопку «ОК». Далее на форме, представленной на рисунке 3.8, нажать кнопку «One variable list» с целью отбора признаков для анализа.
Рисунок 3.6 – Пункты меню для расчета выборочных значений коэффициентов корреляции
Рисунок 3.7 – Форма «Basic Statistics/Tables»
Рисунок 3.8 – Форма расчета коэффициентов корреляции
Для расчета коэффициентов корреляции между каждой парой признаков в окне, представленном на рисунке 3.9, необходимо выбрать все признаки (x1–x5) и нажать кнопку «ОК».
Рисунок 3.9 – Окно выбора признаков для оценивания коэффициентов корреляции
Затем в форме, представленной на рисунке 3.8, нажать кнопку «Summary: Correlations». Результаты расчета представлены на рисунке 3.10, где по каждой переменной выводится ее среднее значение, стандартное отклонение, а также коэффициенты корреляции, при этом красным выделяются те, гипотеза о незначимости которых отвергается.
Рисунок 3.10 – Результаты расчета корреляционной матрицы
После выбора переменных для анализа можно уточнить, в какой форме пользователь желает получить информацию. Имеются три варианта вывода информации, которые выбираются нажатием кнопки «Options» в форме, представленной на рисунке 3.8. Выбор «Display simple matrix (highlight p′s)» в форме, представленной на рисунке 3.11, позволит получить наиболее кратную информацию, в которой приводятся только значения коэффициентов корреляции (рисунок 3.12).
Рисунок 3.11 – Выбор различных вариантов вывода информации о коэффициентах корреляции
Рисунок 3.12 – Значения коэффициентов корреляции
С помощью «Display r, p-levels, and N′s» (рисунок 3.11) можно получить информацию об оценках коэффициентов корреляции, аналогичную предыдущей, но кроме этого приводятся вероятности принятия гипотезы о незначимости коэффициентов (рисунок 3.13).
Рисунок 3.13 – Оценки коэффициентов корреляции и вероятности принятия гипотезы о незначимости коэффициентов
Выбор «Display detailed table of results» (рисунок 3.11) позволит получитьнаиболее подробную информацию: для каждой переменной выводится ее среднее значение (Mean), стандартное отклонение (Std.Dv), объем выборочной совокупности (N), переменные сгруппированы в пары, для каждой из которых выводится коэффициент корреляции (r(X,Y)), его квадрат (r?), наблюдаемое значение t -статистики (t), предназначенное для проверки гипотезы о незначимости коэффициента, вероятность принятия этой гипотезы (p), а также коэффициенты для линейного уравнения регрессии (рисунок 3.14).
Рисунок 3.14 – Значения основных описательных характеристик, коэффициентов корреляции и результаты проверки гипотезы об их незначимости
Таким образом, в результате расчетов получена оценка корреляционной матрицы вида:
Анализируя выборочные значения коэффициентов корреляции, есть основания предполагать наличие: - прямой тесной зависимости между такими парами показателей, как общий коэффициент рождаемости и общий коэффициент брачности ( - прямой заметной связи между удельным весом населения, проживающего в коммунальных квартирах и удельным весом женщин с одним ребенком ( - обратной заметной зависимости между общим коэффициентом рождаемости и удельным весом женщин с одним ребенком ( Между остальными показателями предположительно наблюдается слабая зависимость. Поскольку коэффициенты корреляции отражают взаимосвязь между двумя признаками под воздействием всех остальных, то следующим этапом исследования будет оценка связи между парой признаков, очищенной от влияния всех остальных признаков. Для расчета оценок частных и множественных коэффициентов корреляции необходимо выбрать пункт меню «Statistics», подпункт «Multiple Regression» (рисунок 3.15). В появившейся форме нажать кнопку «Variables», слева выбрать один признак (например, x1), справа все остальные (например, x2–x5) и нажать кнопку «ОК» (рисунок 3.16).
Рисунок 3.15 – Выпор пунктов меню для расчета частных и множественных коэффициентов корреляции
Рисунок 3.16 – Выбор исходных признаков для расчета частных и множественных коэффициентов корреляции
В появившейся форме, представленной на рисунке 3.17, содержится информация о значении множественного коэффициента корреляции
Рисунок 3.17 – Результаты оценивания множественного коэффициента корреляции
Для расчета оценок частных коэффициентов корреляции на текущей форме (рисунок 3.17) необходимо нажать кнопку «Partial correlations», после чего на экране появится форма с выборочными значениями частных коэффициентов корреляции (
Рисунок 3.18 – Результаты оценивания частных коэффициентов корреляции
Аналогичным образом рассчитываются оценки остальных частных коэффициентов корреляции (рисунки 3.19-3.21) и множественных коэффициентов корреляции (рисунки 3.22-3.25).
Рисунок 3.19 – Результаты оценивания частных коэффициентов корреляции
Рисунок 3.20 – Результаты оценивания частных коэффициентов корреляции
Рисунок 3.21 – Результаты оценивания частного коэффициента корреляции
Таким образом, оценки частных коэффициентов корреляции составили:
Сравнивая по абсолютной величине оценки коэффициентов корреляции и соответствующих частных коэффициентов корреляции, можно сделать следующие выводы: например, поскольку
Рисунок 3.22 – Результаты оценивания множественного коэффициента корреляции
Рисунок 3.23 – Результаты оценивания множественного коэффициента корреляции
Рисунок 3.24 – Результаты оценивания множественного коэффициента корреляции
Рисунок 3.25 – Результаты оценивания множественного коэффициента корреляции
Таким образом, оценки множественных коэффициентов корреляции и коэффициентов детерминации составили:
Следующей задачей корреляционного анализа является проверка значимости характеристик связи (коэффициентов корреляции, частных коэффициентов корреляции и коэффициентов детерминации) на уровне значимости Для проверки значимости коэффициентов корреляции воспользуемся результатами, полученными ранее в формах на рисунках 3.13-3.14. Критическое значение
Рисунок 3.26 – Нахождение критического значения для проверки значимости коэффициента корреляции в пакете Excel
Учитывая заданный уровень значимости Результаты проверки гипотез о незначимости коэффициентов корреляции представлены в таблице 3.1. Аналогичным образом на основе информации, представленной на рисунках 3.18-3.21, проверим значимость частных коэффициентов корреляции. При
Рисунок 3.27 – Нахождение критического значения для проверки значимости частного коэффициента корреляции в пакете Excel
Таблица 3.1 – Результаты проверки гипотез о незначимости коэффициентов корреляции
Таблица 3.2 – Результаты проверки гипотез о незначимости частных коэффициентов корреляции
Воспользовавшись результатами, полученными на рисунках 3.17, 3.22-3.25, проверим значимость коэффициентов детерминации (таблица 3.3). Критическое значение
Рисунок 3.28 – Нахождение критического значения для проверки значимости коэффициента детерминации в пакете Excel
Учитывая заданный уровень значимости
Таблица 3.3 – Результаты проверки гипотез о незначимости коэффициентов детерминации
Следующим этапом корреляционного анализа является построение с вероятностью Рассмотрим пример построения доверительного интервала для статистически значимого коэффициента корреляции Осуществим над
Рисунок 3.29 – Осуществление z -преобразования Фишера в пакете Excel
Получим
где Учитывая, что
Рисунок 3.30 – Определение квантили стандартного нормального закона распределения в пакете Excel
Получили
Для получения доверительного интервала для
Рисунок 3.31 – Осуществление обратного z -преобразования Фишера для левой границы доверительного интервала в пакете Excel
Получили, что нижняя граница доверительного интервала для
Рисунок 3.32 – Осуществление обратного z -преобразования Фишера для правой границы доверительного интервала в пакете Excel
Верхняя граница доверительного интервала для
Аналогичным образом строятся доверительные интервалы для остальных статистически значимых коэффициентов корреляции (таблица 3.4) и частных коэффициентов корреляции (таблица 3.5).
Таблица 3.4 – Результаты построения доверительных интервалов для значимых коэффициентов корреляции
Таблица 3.5 – Результаты построения доверительных интервалов для значимых частных коэффициентов корреляции
Заключительным этапом корреляционного анализа является оценка уравнения регрессии. Исходя из экономических соображений, выберем в качестве результативного признака показатель
будут выступать в качестве факторов, оказывающих влияние на общий коэффициент рождаемости. Для оценки уравнения регрессии
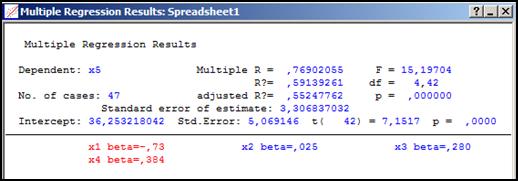
воспользуемся пунктом меню «Statistics», подпунктом «Multiple Regression» (рисунок 3.15). В появившейся форме, представленной на рисунке 3.16, после нажатия кнопки «Variables», слева выбираем признак x1, справа все остальные x2–x5 и нажимаем кнопку «ОК». Для получения оценки уравнения регрессии на форме, представленной на рисунке 3.17, необходимо нажать кнопку «Summary: Regression results». Вид формы с результатами оценки уравнения регрессии представлен на рисунке 3.33.
Рисунок 3.33 – Результаты оценки уравнения регрессии
Таким образом, оценка уравнения регрессии имеет вид:
Уравнение регрессии для признака Таким образом, корреляционно-регрессионный анализ показателей социально-демографического положения региона позволил сделать следующие выводы. 1) В среднем по Оренбургской области общий коэффициент рождаемости составил 16,42‰; общий коэффициент брачности – 9,29‰; в среднем на территории Оренбургской области проживает 9,26% казахского населения; средний по региону удельный вес населения, проживающего в коммунальных квартирах, составил 0,51%; удельный вес женщин с одним ребенком – 20,37% к общему числу женщин с детьми. 2) Анализ коэффициентов корреляции показал, что на 5%-ом уровне значимости статистически значимая тесная прямая зависимость наблюдается между следующими парами признаков: общий коэффициент рождаемости и общий коэффициент брачности ( 3) Сравнивая по абсолютной величине оценки коэффициентов корреляции и соответствующих частных коэффициентов корреляции, можно сделать вывод, что во всех случаях показатели, влияние которых устраняет
|

 – общий коэффициент рождаемости (‰);
– общий коэффициент рождаемости (‰); – общий коэффициент брачности (‰);
– общий коэффициент брачности (‰);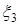 – удельный вес казахского населения (%);
– удельный вес казахского населения (%); – удельный вес населения, проживающего в коммунальных квартирах (%);
– удельный вес населения, проживающего в коммунальных квартирах (%); – удельный вес женщин с одним ребенком (в % к общему числу женщин с детьми).
– удельный вес женщин с одним ребенком (в % к общему числу женщин с детьми).






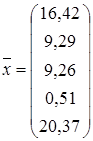 – вектор средних значений признаков;
– вектор средних значений признаков; – оценка ковариационной матрицы.
– оценка ковариационной матрицы. ), т.е. рост удельного веса населения, проживающего в коммунальных квартирах способствует сокращению уровня рождаемости.
), т.е. рост удельного веса населения, проживающего в коммунальных квартирах способствует сокращению уровня рождаемости.








 .
. ); общий коэффициент рождаемости и удельный вес казахского населения (
); общий коэффициент рождаемости и удельный вес казахского населения (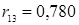 ), а также общий коэффициент брачности и удельный вес казахского населения (
), а также общий коэффициент брачности и удельный вес казахского населения ( );
); );
); ), а также обратной умеренной связи между общим коэффициентом брачности и удельным весом женщин с одним ребенком (
), а также обратной умеренной связи между общим коэффициентом брачности и удельным весом женщин с одним ребенком ( ).
).

 , коэффициента детерминации
, коэффициента детерминации  , а также значение F -статистики, предназначенной для проверки гипотезы о незначимости коэффициента детерминации (
, а также значение F -статистики, предназначенной для проверки гипотезы о незначимости коэффициента детерминации ( ) и вероятности принятия данной гипотезы (
) и вероятности принятия данной гипотезы ( ).
).


 и коэффициента детерминации
и коэффициента детерминации 
 ,
,  ,
, 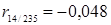 ,
,  ), содержащихся во втором столбце таблицы, представленной на рисунке 3.18.
), содержащихся во втором столбце таблицы, представленной на рисунке 3.18.
 ,
,  ,
,  ,
, 

 ,
,  ,
, 

 ,
, 








 ), удельный вес населения, проживающего в коммунальных квартирах (
), удельный вес населения, проживающего в коммунальных квартирах ( ) усиливают взаимосвязь между общим коэффициентом рождаемости (
) усиливают взаимосвязь между общим коэффициентом рождаемости ( ) и общим коэффициентом брачности (
) и общим коэффициентом брачности (
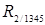 и коэффициента детерминации
и коэффициента детерминации 

 и коэффициента детерминации
и коэффициента детерминации 

 и коэффициента детерминации
и коэффициента детерминации 
 и коэффициента детерминации
и коэффициента детерминации 


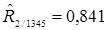

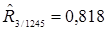





 , которая может быть осуществлена двумя способами. Первый способ основан на сравнении наблюдаемого значения статистики с критическим значением, при этом если
, которая может быть осуществлена двумя способами. Первый способ основан на сравнении наблюдаемого значения статистики с критическим значением, при этом если  (для коэффициентов корреляции и частных коэффициентов корреляции),
(для коэффициентов корреляции и частных коэффициентов корреляции),  (для коэффициентов детерминации), тос вероятность ошибки 0,05 нулевая гипотеза о незначимости соответствующих характеристик связи отклоняется. Второй способ предполагает сравнение значения вероятности принятия нулевой гипотезы о незначимости характеристики связи (наблюдаемого уровня значимости p) с заранее заданным уровнем значимости
(для коэффициентов детерминации), тос вероятность ошибки 0,05 нулевая гипотеза о незначимости соответствующих характеристик связи отклоняется. Второй способ предполагает сравнение значения вероятности принятия нулевой гипотезы о незначимости характеристики связи (наблюдаемого уровня значимости p) с заранее заданным уровнем значимости  , при этом, если
, при этом, если  , то на 5%-ом уровне значимости нулевая гипотеза отклоняется и делается вывод о статистической значимости соответствующих характеристик связи.
, то на 5%-ом уровне значимости нулевая гипотеза отклоняется и делается вывод о статистической значимости соответствующих характеристик связи. определим с помощью функции Excel СТЬЮДЕНТ.ОБР.2Х (Вероятность;Степени_свободы) (рисунок 3.26).
определим с помощью функции Excel СТЬЮДЕНТ.ОБР.2Х (Вероятность;Степени_свободы) (рисунок 3.26).
 , критическая точка принимает следующее значение
, критическая точка принимает следующее значение  .
. , критическая точка принимает следующее значение
, критическая точка принимает следующее значение  (рисунок 3.27). Результаты проверки сведены в таблицу 3.2.
(рисунок 3.27). Результаты проверки сведены в таблицу 3.2.


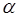













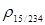






 определим с помощью функции F.ОБР.ПХ(Вероятность;Степени_свободы1;Степени_свободы2) пакета Excel (рисунок 3.28).
определим с помощью функции F.ОБР.ПХ(Вероятность;Степени_свободы1;Степени_свободы2) пакета Excel (рисунок 3.28).
 ,
,  , критическая точка принимает следующее значение
, критическая точка принимает следующее значение  .
.




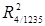

 доверительных интервалов для значимых коэффициентов корреляции и частных коэффициентов корреляции с помощью z -преобразования Фишера.
доверительных интервалов для значимых коэффициентов корреляции и частных коэффициентов корреляции с помощью z -преобразования Фишера. .
. , для этого воспользуемся функцией ФИШЕР(X) пакета Excel (рисунок 3.29).
, для этого воспользуемся функцией ФИШЕР(X) пакета Excel (рисунок 3.29).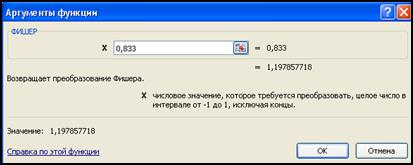
 . Далее строится доверительный интервал для
. Далее строится доверительный интервал для  :
: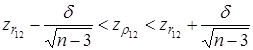 ,
, – квантиль уровня
– квантиль уровня  стандартного нормального закона распределения.
стандартного нормального закона распределения. стандартного нормального закона распределения, воспользовавшись функцией НОРМ.СТ.ОБР(вероятность) пакета Excel (рисунок 3.30).
стандартного нормального закона распределения, воспользовавшись функцией НОРМ.СТ.ОБР(вероятность) пакета Excel (рисунок 3.30).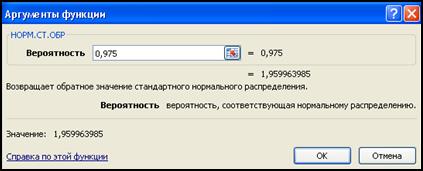
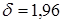 , после чего определим границы доверительного интервала для
, после чего определим границы доверительного интервала для  или
или  .
.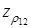 осуществим преобразование, обратное z -преобразованию Фишера, для чего воспользуемся функцией ФИШЕРОБР(Y) пакета Excel (рисунки 3.31-3.32).
осуществим преобразование, обратное z -преобразованию Фишера, для чего воспользуемся функцией ФИШЕРОБР(Y) пакета Excel (рисунки 3.31-3.32).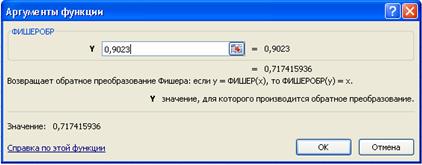

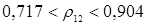 .
. ). Остальные признаки:
). Остальные признаки: – общий коэффициент брачности;
– общий коэффициент брачности; – удельный вес населения, проживающего в коммунальных квартирах;
– удельный вес населения, проживающего в коммунальных квартирах;


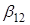 ,
,  ,
,  , поскольку значимы соответствующие частные коэффициенты корреляции
, поскольку значимы соответствующие частные коэффициенты корреляции  , при этом
, при этом  с вероятностью 0,95 не меньше 0,717 и не больше 0,904), общий коэффициент рождаемости и удельный вес казахского населения (
с вероятностью 0,95 не меньше 0,717 и не больше 0,904), общий коэффициент рождаемости и удельный вес казахского населения ( , с вероятностью 0,95
, с вероятностью 0,95  не меньше 0,635 и не больше), а также общий коэффициент брачности и удельный вес казахского населения (
не меньше 0,635 и не больше), а также общий коэффициент брачности и удельный вес казахского населения ( , с вероятностью 0,95
, с вероятностью 0,95  не меньше 0,547 и не больше 0,835). Прямая связь заметной силы существует между удельным весом населения, проживающего в коммунальных квартирах, и удельным весом женщин с одним ребенком (
не меньше 0,547 и не больше 0,835). Прямая связь заметной силы существует между удельным весом населения, проживающего в коммунальных квартирах, и удельным весом женщин с одним ребенком ( , с вероятностью 0,95
, с вероятностью 0,95  не меньше 0,394 и не больше 0,765); обратная зависимость заметной силы – между общим коэффициентом рождаемости и удельным весом женщин с одним ребенком (
не меньше 0,394 и не больше 0,765); обратная зависимость заметной силы – между общим коэффициентом рождаемости и удельным весом женщин с одним ребенком ( , с вероятностью 0,95
, с вероятностью 0,95  не меньше -0,779 и не больше -0,424), обратная зависимость умеренной силы – между общим коэффициентом брачности и удельным весом женщин с одним ребенком (
не меньше -0,779 и не больше -0,424), обратная зависимость умеренной силы – между общим коэффициентом брачности и удельным весом женщин с одним ребенком ( , с вероятностью 0,95
, с вероятностью 0,95  не меньше -0,683 и не больше -0,240). Между остальными показателями наблюдается статистически значимая, но сравнительно слабая зависимость; статистически незначимая связь с точки зрения коэффициентов корреляции оказалась между удельным весом казахского населения и удельным весом населения, проживающего в коммунальных квартирах.
не меньше -0,683 и не больше -0,240). Между остальными показателями наблюдается статистически значимая, но сравнительно слабая зависимость; статистически незначимая связь с точки зрения коэффициентов корреляции оказалась между удельным весом казахского населения и удельным весом населения, проживающего в коммунальных квартирах.


