Электрлік ығысу.
Электрлік ығысу (электрлік индукция) өрнегі:
Өлшемсіз шаманы Ε шамасы диэлектриктің электр өрісінде поляризациялануы кезінде диэлектриктің қасиетін сипаттай отырып, электр өрісінің диэлектриктің әсерінен қаншалықты кемитінін көрсетеді. Электрлік ығысу векторының өлшем бірлігі – Кл/м Диэлектриктегі зарядқа әсер ететін күш: Поляризацияланғанда диэлектриктердің деформациялануы электрострикция деп аталады. Тұйықталған бет үшін электрлік ығысу векторын есептеуде Остроградский – Гаусс теоремасы мына түрде жазылады:
Тұйықталған бет арқылы электрлік ығысудың векторлық ағыны осы беттің ішіндегі еркін зарядтардың алгебралық қосындысына тең. Егер еркін зарядтар тұйықталған беттің ішінде
Электр өрісіндегі өткізгіштер. Электр сыйымдылық; Егер электростатикалық өріске өткізгішті ендірсек немесе өткізгішке аздаған заряд берсек, онда электрлік күштердің әсерінен осы зарядтар орын ауыстыра бастайды. Сөйтіп, зарядтар тепе – тең болып бөлінгенге дейін, өткізгіштер қозғалыста болады. Осы кезде өткізгіштің барлық жеріндегі өріс кернеулігі нольге тең болады ( Ол қисықтың оң болғанда (дөңес) тығыздық артады да, теріс болғанда (ойыс) кемиді. Зарядтардың тығыздығы, әсіресе сүйір ұштарда көп болады. Егер өткізгішке бір q заряды берілсе, онда ол өткізгіштің ішіндегі өріс кернеулігі
Мұндағы пропорционалдық коэффициент С өткізгіштердің электр сыйымдылығы деп аталады, ол
Сонымен, сыйымдылық сан жағынан өткізгіштің потенциалын бір өлшемге арттыруға қажетті зарядқа тең екен. Өткізгіштің сыйымдылығы оның формасы мен өлшеміне тәуелді де бірақ өткізгіштің тегіне, агрегаттық күйіне және оның ішкі астарларының өлшемдеріне тәуелсіз. Мұны зарядтардың көпшілігі негізінен өткізгіштің сыртқы беттеріне орналасуынан деп түсінуге болады. Сыйымдылықтың өлшем бірлігіне өткізгішке 1Кл – ға тең заряд бергенде оның потенциалы 1В – ке өзгеретін өткізгіштің сыйымдылығы алынады. Сыйымдылықтың бұл өлшемі Фарад (Ф) деп аталады.
|



 ортаның салыстырмалық диэлектрлік өтімділік немесе жай ғана диэлектрлік өтімділік деп атайды.
ортаның салыстырмалық диэлектрлік өтімділік немесе жай ғана диэлектрлік өтімділік деп атайды. .
.
 (8.5)
(8.5)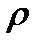 көлемдік тығыздықпен бөлініп таралған болса, онда формула мына түрде өзгереді:
көлемдік тығыздықпен бөлініп таралған болса, онда формула мына түрде өзгереді: . (8.6)
. (8.6) ), себебі, өткізгіш ішіндегі потенциялдар тұрақты болу керек (φ = const). Сонымен қатар өткізгіш бетінің әрбір нүктесіндегі өріс кернеулігі бетке нормаль бойымен бағытталады. Демек, тепе – теңдік жағдайда өткізгіштің беті эквипотенциал болады. Тепе – теңдік кезінде өткізгіш ішіндегі кез келген нүктеде өріс болмағандықтан, бет арқылы электрлік зарядтардың ығысу векторының ағыны
), себебі, өткізгіш ішіндегі потенциялдар тұрақты болу керек (φ = const). Сонымен қатар өткізгіш бетінің әрбір нүктесіндегі өріс кернеулігі бетке нормаль бойымен бағытталады. Демек, тепе – теңдік жағдайда өткізгіштің беті эквипотенциал болады. Тепе – теңдік кезінде өткізгіш ішіндегі кез келген нүктеде өріс болмағандықтан, бет арқылы электрлік зарядтардың ығысу векторының ағыны  нолге тең болады. Ол зарядтардың алгебралық қосындысы да Остроградский – Гаусс теоремасына сәйкес нолге тең. Олай болса, тепе – теңдік кезінде өткізгіштің ішіндегі ешбір жерде артық заряд болуы мүмкін емес, сөйтіп зарядтар өткізгіштің бетінде белгілі бір тығыздықпен (δ) орналасуы керек. Жалпы өткізгіштің берілген потенциялына зарядтардың тығыздығы беттің қисықтығымен анықталады.
нолге тең болады. Ол зарядтардың алгебралық қосындысы да Остроградский – Гаусс теоремасына сәйкес нолге тең. Олай болса, тепе – теңдік кезінде өткізгіштің ішіндегі ешбір жерде артық заряд болуы мүмкін емес, сөйтіп зарядтар өткізгіштің бетінде белгілі бір тығыздықпен (δ) орналасуы керек. Жалпы өткізгіштің берілген потенциялына зарядтардың тығыздығы беттің қисықтығымен анықталады. болатындай таралады. Сондай – ақ өткізгіштегі зарядтың артуы қоршаған денелердегі зарядтардың бөлініп таралуына өзгеріс туғызбаған жағдайда ғана орындалады. Сөйтіп, шамалары әр түрлі зарядтар басқа денелерден оңашаланған өткізгіште осы тәртіппен тарайды. Сонда өткізгіш бетінің кез келген екі нүктесіндегі заряд тығыздықтарының қатынасы зарядтың кез келген шамасы үшін бірдей болады. Бұдан оқшауланған өткізгіштің потенциалы ондағы бар зарядқа пропорционал болатынын көруге болады. Мысалы, өткізгіштегі зарядты қанша есе арттырсақ, онда өрістің әрбір нүктесіндегі кернеулігінің де сонша есеге артатынын байқаймыз. Олай болса, бірлік зарядты шексіздіктен өткізгіштің бетіне алып келу үшін істелген жұмыс және оның потенциалы еселеп артады. Сонымен, оқшауланған өткізгіш үшін:
болатындай таралады. Сондай – ақ өткізгіштегі зарядтың артуы қоршаған денелердегі зарядтардың бөлініп таралуына өзгеріс туғызбаған жағдайда ғана орындалады. Сөйтіп, шамалары әр түрлі зарядтар басқа денелерден оңашаланған өткізгіште осы тәртіппен тарайды. Сонда өткізгіш бетінің кез келген екі нүктесіндегі заряд тығыздықтарының қатынасы зарядтың кез келген шамасы үшін бірдей болады. Бұдан оқшауланған өткізгіштің потенциалы ондағы бар зарядқа пропорционал болатынын көруге болады. Мысалы, өткізгіштегі зарядты қанша есе арттырсақ, онда өрістің әрбір нүктесіндегі кернеулігінің де сонша есеге артатынын байқаймыз. Олай болса, бірлік зарядты шексіздіктен өткізгіштің бетіне алып келу үшін істелген жұмыс және оның потенциалы еселеп артады. Сонымен, оқшауланған өткізгіш үшін: , (8.7)
, (8.7) . (8.8)
. (8.8)


