Электр өрісінің энергиясы
1. Зарядтар жүйесінің энрегиясы. Зарядталған денелердің өзара әсер күштері консервативті болғандықтан зарядтар жүйесінің потенциалдық энергиясы болады. Зарядтар жүйесінің энергиялары өзара тең Зарядтар жүйесіне тағы да басқа бірнеше n зарядтарды қоссақ, n заряд жағдайында жүйенің потенциалдық энергиясы мынаған тең болады: 2. зарядталған өткізгіштің энергиясы. Егер де бір оқшауланған өткізгіштің заряды q болса, онда оның маңында электростатикалық өріс пайда болады. Осы өткізгіш бетінің потенциалы φ де, сыйымдылығы С болсын. Енді өткізгіштің зарядын dq –ге арттырайық. Сонда осы dq зарядты шексіздіктен жақындатсақ, ондағы істелінген жұмыстың шамасы:
Осы жұмыс өткізгіштің энергиясын арттыруға кетеді:
Өткізгіштің беті эквипотенциалды болғандықтан, нүктелік заряд орналасқан нүктелердің потенциалы бірдей әрі өткізгіштің потенциалына тең болады, сондықтан энергия:
Мұндағы 3. Зарядталған өрісінің энергиясы. Кез келген өткізгіштер сияқты, зарядталған конденсаторлардың да энергиялары болады да, ол энергияның шамасы:
Мұндағы С – конденсатордың сыйымдылығы, q – оның астарларындағы зарядтың шамасы: 4.. Электр өрісінің энергиясы Энергияның тығыздығы. Зарядталған конденсатор энергиясын оның астарларындағы электростатикалық өрісті сипаттайтын шамамен өрнектеуге болады. Ол үшін жазық конденсатор сыйымдылығының мәнін Конденсатор астарлары арасындағы потенциалдар айырымының оның кернеулігімен байланысын
Мұндағы V = Sd өрістің алып тұрған көлемі. Енді өріс біртекті болғанда, ондағы энергия кеңістікте тұрақты ω тығыздықпен тарайды деп, өрістің энергиясын сол өріс толып тұрған көлемге (V) бөлейік:
|

 , сондықтан зарядтар жүйесінің энергиясы мынаған тең:
, сондықтан зарядтар жүйесінің энергиясы мынаған тең: 

 , бірақ
, бірақ  болғандықтан, жұмыс
болғандықтан, жұмыс  . Толық жұмысты табу үшін осы өрнекті потенциалы 0 – ден φ – ге дейін өзгеретіндей етіп интегралдаймыз:
. Толық жұмысты табу үшін осы өрнекті потенциалы 0 – ден φ – ге дейін өзгеретіндей етіп интегралдаймыз:
 (8.9)
(8.9)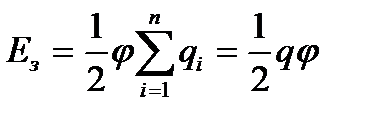 . (8.10)
. (8.10) - өткізгіштегі зарядтар.
- өткізгіштегі зарядтар. , (8.11)
, (8.11) - конденсатор астарларының арасындағы потенциалдар айырмасы.
- конденсатор астарларының арасындағы потенциалдар айырмасы. осы өрнегіне қойып, оның өрісіндегі энергияны табуға болады:
осы өрнегіне қойып, оның өрісіндегі энергияны табуға болады:  .
. екенін ескеріп, соңғы өрнекгін мына түрде жазамыз:
екенін ескеріп, соңғы өрнекгін мына түрде жазамыз: . (8.12)
. (8.12) Бұл өрнек электр өрісі энергиясының тығыздығының өрнегі деп аталады. Электрлік ығысу векторының мәнін, яғни
Бұл өрнек электр өрісі энергиясының тығыздығының өрнегі деп аталады. Электрлік ығысу векторының мәнін, яғни  екенін ескеріп, тығыздықты басқа түрде өрнектеуге болады:
екенін ескеріп, тығыздықты басқа түрде өрнектеуге болады: 



