ЗАДАННЫМИ ТОЧКАМИ А И В
Величина среднего уклона линии АВ вычисляется по формуле: iCP =
где НА, НB − отметки точек А и В; dAB −; длина горизонтального отрезка АВ на местности. На рис. 62. НА = 125,0; H в = 112,5.
dAB=L·M, где L − длина отрезка на карте, см; М − знаменатель численного масштаба карты. L = 5,73 см; М = 10000; d = 5,73 ∙ 100 = 573 м; iCP = здесь 0,001 = 1 − одна промилле (тысячная). Для определения минимального и максимального уклонов проанализируем формулу вычисления уклонов: i= Если в этой формуле взять h = hС (высота сечения рельефа), а d = = а (расстояние между соседними горизонталями называется заложением), т.е.: i = то анализ этой формулы свидетельствует о том, что при одной и той же высоте сечения рельефа уклон меньше на том участке, где расстояние между горизонталями больше, и наоборот, наименьшему заложению соответствует наибольший уклон. Выбрав вдоль линии АВ участки с максимальным и минимальным заложениями amin, amax, вычислим соответствующие им уклоны: i = Минимальный и максимальный уклоны можно определить, используя график масштаба заложений, который строится обычно на планах для уклонов, а на картах − для углов наклона местности. Если график масштаба заложений на карте или плане отсутствует, то его легко можно построить, для этого необходимо из формулы (i = а = Задавая i различные значения, имеющие место на данной карте или плане, вычисляют значения а 1, а 2, а 3, а 4и т. д. Например: i 1= 0,01; i 2 = 0,02; i 3 = 0,03; i 4 = 0,04 и т. д. Получим при hc = 2,5 м; а 1= 250 м; а 2= 125 м; а 3= 83 м; а 4= 63 м; а 5 = 50 м и т. д. Для карты масштаба 1:10000 получим отрезки а в см: а 1 = 2,5 см; а 2 = 1,25 см; а 3 = 0,8 см; а 4 = 0,6 см; а 5 = 0,5 см и т. д. График строят следующим образом (рис. 63): − на горизонтальной линии подписывают значение i через равные промежутки; − на перпендикулярах, построенных из точек, соответствующих оцифрованным значениям i, откладывают отрезки а 1, а 2, а 3 и т. д. и соединяют концы отрезков плавной кривой.
М 1:10000 Рис. 63. График масштаба заложений для уклонов, hc = 2,5 м. Аналогично можно построить масштаб заложений для определения углов наклона (рис. 64). Так как: i = отсюда а = Задаваясь различными значениями v, вычислим а 1, а 2, а 3 и т. д. Например, при v 1 = 0º30'; v 2 = lº; v 3 = 2º; v 4 = 3º; v 5 = 4º и масштабе 1:10000 получим: а 1= 573 м; а 2 = 286 м; а 3 = 143 м; а 4 = 95 м; а 5 = 71 м; а 6 = 57 м; а 7 = 48 м; а 8 = 41 м; а 9= 36 м. Или в масштабе карты: а 1 = 5,7 см; а 2 = 2,8 см; а 3 = 1,4 см; а 4 = 0,9 см и т. д.
М 1:10000 Рис. 64. График масштаба заложений для углов наклона, hc = 5 м. Пользуются графиком масштаба заложений следующим образом: − по линии АВ выбирают минимальное расстояние между горизонталями и берут это расстояние в раствор циркуля; − циркуль прикладывают к графику таким образом, чтобы одна игла двигалась по горизонтальной линии до тех пор, пока вторая игла не окажется на кривой. На рис. 62 максимальный уклон вдоль линии АВ равен 2º48'; минимальный − 2º 12'.
ПОСТРОЕНИЕ ТОПОГРАФИЧЕСКОГО ПЛАНА ПОЛИГОНА
|

 ;
; = − 0,0218 ≈ 22 ‰.
= − 0,0218 ≈ 22 ‰.

 = 0,125 = 125 ‰.
= 0,125 = 125 ‰.

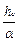 = tgv,
= tgv, = hc ∙ ctg v.
= hc ∙ ctg v.



