Основное понятия, явление дифракции
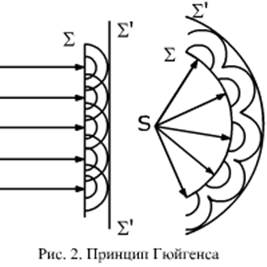
I Теоретическая часть Основное понятия, явление дифракции Поместим на пути параллельного пучка света плоскость и будем наблюдать дальнейший ход распространения световых лучей на экране Е. Если бы волна представляла собой действительно пучок параллельных прямых, то тень от объекта, поставленного на пути её распространения, должна была бы иметь на экране совершенно четкие контуры. Это было предсказано геометрической оптикой и подтверждено грубыми опытам. Однако наиболее тщательное изучение показывает, что в действительности край тени не является резким, а состоит из чередующихся в последовательности светлых и темных полос. То жесамое явление наблюдается, если на пути луча поместить круглое отверстие или щель. Контур получаемой на экране тени оказывается окаймлённым светлыми и тёмными полосами, тем более заметными, чем меньше размеры отверстий. Это "явление" огибания края препятствия волной называется дифракцией и проявляется всякий раз, когда на пути распространения фронт волны тем или иным способом ограничивается. Явление дифракции, которое не могла объяснить геометрическая оптика, находится в тесной связи с явлением интерференции и может быть объяснено на основании принципа Гюйгенса. Согласно принципу Гюйгенса каждую точку волновой поверхности следует рассматривать как источник элементарных сферических волн, огибающая их поверхность служит новой волновой поверхностью (рис.2). Объясним явление дифракции на краю плоскости Р, на основании принципа Гюйгенса. Волновая поверхность Еявляется источником, вторичных сферических волн (рис.3). Каждая точка поверхности Е эмитирует световые волны в различных направлениях. Выберем те лучи, которые собираются в точке экрана. Эти лучи когерентны, т.е. имеют одинаковую частоту и постоянную разность фаз, и, следовательно, могут
интерферировать. Если лучи приходят в точку Р в фазе, то происходит усиление света и мы наблюдаем светлую полосу. В некоторую точку Аналогично можно, объяснить явление дифракции на щели на круглом отверстии и на других преградах.
Пусть решётка R освещается параллельным и нормальным к решётке пучком световых волн длинной Лучи собираются в точке P, экрана E, расположенного в фокальной плоскости линзы L. Разность хода
Если разность хода равна целому числу длин волн
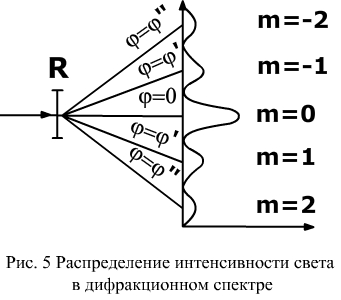
где m-порядок спектра, φ; - угол дифракции. В направлениях, не удовлетворяющих соотношению (2), наблюдаются темные полосы. В результате дифракционная картина представляет собой чередование темных и светлых полос.
На некотором расстоянии от главного максимума расположены максимумы первого порядка (m= Интенсивность светлых полос уменьшается с увеличением порядка. Количество наблюдаемых на экране дифракционных максимумов определяется периодом решетки.
|


 лучи приходят в противофазе и происходит взаимное ослабление света. Тогда в точке
лучи приходят в противофазе и происходит взаимное ослабление света. Тогда в точке  Рассмотрим, например, явление дифракции на дифракционной решётке. Решётка состоит из большого числа параллельных и разностоящих друг от друга щелей (рис.4а). Ширина щели по величине должна быть одного порядка с длинной волны света, ширина непрозрачного участка также невелика. Для соблюдения этих условий линейная плотность штрихов на решётке должна составлять сотни штук на миллиметр. Суммарная ширина прозрачного и непрозрачного участков решётки называется ее период
Рассмотрим, например, явление дифракции на дифракционной решётке. Решётка состоит из большого числа параллельных и разностоящих друг от друга щелей (рис.4а). Ширина щели по величине должна быть одного порядка с длинной волны света, ширина непрозрачного участка также невелика. Для соблюдения этих условий линейная плотность штрихов на решётке должна составлять сотни штук на миллиметр. Суммарная ширина прозрачного и непрозрачного участков решётки называется ее период 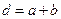 (рис.4б).
(рис.4б). . Каждая из щелей является источником вторичных волн, излучающих свет по различным направлениям. Произвольно выберем одно из них, направленное под углом
. Каждая из щелей является источником вторичных волн, излучающих свет по различным направлениям. Произвольно выберем одно из них, направленное под углом  к нормали решётки (рис.4а).
к нормали решётки (рис.4а). двух любых соседних лучей равна:
двух любых соседних лучей равна: (1)
(1) (где m=0,
(где m=0,  , то лучи, распространяющиеся в направлении удовлетворяющему условию
, то лучи, распространяющиеся в направлении удовлетворяющему условию  (2)
(2) При
При 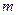 =0).
=0). ), второго порядка (m=
), второго порядка (m=  ) и т.д.
) и т.д.


