1.Установить решетку на рельсе 3 между лазером и экраном
2. Измерить расстояние  от главного максимума до максимумов
от главного максимума до максимумов  ,
, 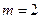 порядков. Для вычисления длины волны используем формулу (2)
порядков. Для вычисления длины волны используем формулу (2)
 (3)
(3)
где 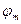 - угол дифракции m-го порядка
- угол дифракции m-го порядка
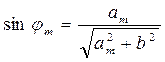
где b – расстояние от решётки до экрана.
 (4)
(4)

 - ошибка определения b и
- ошибка определения b и  , равны
, равны  цены деления линеек.
цены деления линеек.
2.3 Определение периода решётки
1.Установить решётку с неизвестным периодом на рельс на расстояние 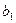 от экрана.
от экрана.
2.Измерить расстояние  от главного максимума до максимума 1-го порядка. 3.Установить решётку на расстоянии
от главного максимума до максимума 1-го порядка. 3.Установить решётку на расстоянии  и измерить расстояние
и измерить расстояние  до максимума 2-го порядка.
до максимума 2-го порядка.
4. Для расстояния 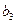 измерить
измерить  для максимума 3-го порядка.
для максимума 3-го порядка.
5. Рассчитать 3 значения периода решётки  по формуле:
по формуле:

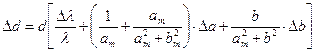
Вычислить среднее значение периода дифракционной решетки,  и
и 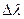 брать из предыдущих результатов
брать из предыдущих результатов
Лабораторная работа
“Дифракция на решетке”
Целью работы является ознакомление с дифракцией на периодических структурах и экспериментальное определение количественных соотношений между геометрическими параметрами дифрагирующего объекта, оптической системы, дифракционной картины и длиной волны излучения.
Основные сведения из теории.
К дифракции света относятся любые отклонения от правил и соотношений, определяемых приближением геометрической оптики, т.е. в тех случаях, когда длиной волны излучения нельзя пренебречь и волновые свойства света играют доминирующую роль. Одним из наиболее ярких дифракционных эффектов является дифракция на решетке. Этот эффект является частным случаем дифракции на пространственных периодических структурах, к которым относятся в частности: дифракция рентгеновских лучей в кристаллах, дифракция света на стоячих волнах в акустооптических модуляторах и других. Теория дифракции на таких структурах лежит в основе когерентной оптики и, в частности, теории Аббе образования изображения в микроскопе.
В основе волновой теории света лежит принцип Гюйгенса - Френеля, основная идея которого состоит в том, что каждая точка волнового фронта является источником вторичных сферических волн, а амплитуда и фаза этого источника равны соответственно амплитуде и фазе пришедшей в данную точку волны. Напряженность электромагнитного поля в произвольной точке пространства равна сумме напряженностей полей от каждого вторичного источников, достигших этой точки. Радиусы кривизны этих волн зависит от расстояния от данной точки до источников и на достаточно большем удалении точки волны можно считать плоскими. Такая ситуация называется дифракцией в приближении Фраунгофера или дифракцией в плоских волнах. Условием такого приближения является то, что размер объекта, на котором происходит дифракция 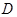 , расстояние от объекта до точки наблюдения
, расстояние от объекта до точки наблюдения  и длина волны излучения
и длина волны излучения 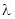 связаны соотношением
связаны соотношением
 , (1)
, (1)
где выражение  является радиусом первой зоны Френеля. Если выполняется такое условие, то говорят, что наблюдения проводятся в дальней зоне.
является радиусом первой зоны Френеля. Если выполняется такое условие, то говорят, что наблюдения проводятся в дальней зоне.
Математически, принцип Гюйгенса - Френеля в приближении Фраунгофера записывается с помощью интеграла
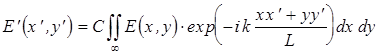 , (2)
, (2)
где 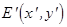 ,
,  - распределения комплексных амплитуд в плоскости наблюдения и в плоскости объекта, где происходит дифракция, соответственно;
- распределения комплексных амплитуд в плоскости наблюдения и в плоскости объекта, где происходит дифракция, соответственно; 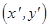 ,
,  - координаты в отмеченных выше плоскостях;
- координаты в отмеченных выше плоскостях;  - расстояние между этими плоскостями;
- расстояние между этими плоскостями; 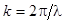 - волновое число;
- волновое число; 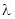 - длина волны излучения;
- длина волны излучения; 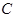 - константа, зависящая от расстояния, влияющая лишь на общую яркость дифракционного распределения, но никак не сказывающейся на его структуре (это так называемая нормировочная постоянная, ее можно положить равной единице и мы в дальнейшем будем ее опускать). В этом выражении предполагается бесконечная область интегрирования, однако на практике эта область фактически конечна: она либо ограничена непрозрачным экраном (или несколькими экранами), либо поле сосредоточено в некоторой области, хотя спадая, простирается до бесконечности (например, по экспоненциальному закону). Площадь этой области
- константа, зависящая от расстояния, влияющая лишь на общую яркость дифракционного распределения, но никак не сказывающейся на его структуре (это так называемая нормировочная постоянная, ее можно положить равной единице и мы в дальнейшем будем ее опускать). В этом выражении предполагается бесконечная область интегрирования, однако на практике эта область фактически конечна: она либо ограничена непрозрачным экраном (или несколькими экранами), либо поле сосредоточено в некоторой области, хотя спадая, простирается до бесконечности (например, по экспоненциальному закону). Площадь этой области 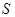 определяет размер объекта, на котором происходит дифракция (
определяет размер объекта, на котором происходит дифракция ( ).
).
Рассмотрим дифракцию Фраунгофера от некоторого объекта. Этот объект влияет на проходящее сквозь него излучение, изменяя его амплитуду и фазу, и может быть описан комплексной функцией пропускания.
 , (3)
, (3)

|
| рис 1.а амплитудная структура
|

|
| рис 1.б фазовая структура
|

|
| рис 1.в амплитудно - фазовая структура
|
где  - амплитудное пропускание, определяемое прозрачностью объекта в точке
- амплитудное пропускание, определяемое прозрачностью объекта в точке  ,
,  - фазовое пропускание, которое в частности связано с функцией профиля одной из поверхностей объекта
- фазовое пропускание, которое в частности связано с функцией профиля одной из поверхностей объекта  (если другая поверхность плоская) соотношением
(если другая поверхность плоская) соотношением
 , (4)
, (4)
где  - показатель преломления вещества объекта,
- показатель преломления вещества объекта, 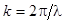 - волновое число. Если на объект падает волна с комплексным распределением амплитуд
- волновое число. Если на объект падает волна с комплексным распределением амплитуд
 , (5)
, (5)
то после прохождения объекта, распределение комплексных амплитуд 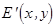 станет
станет
 , (6)
, (6)
т.е. распределение амплитуд поля 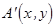 и фаз
и фаз  после объекта будут
после объекта будут
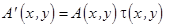 ,
, 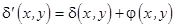 . (7)
. (7)
В соответствии со сказанным, периодические структуры, называемые еще решетками, бывают трех типов - амплитудные, фазовые и амплитудно-фазовые. На рисунках (рис 1.а, 1.б, 1.в) показаны сечения таких структур (решеток). Очевидно, что амплитудно-фазовая решетка является обобщением периодических структур, так как два других типа решеток являются ее частными случаями.
Рассмотрим дифракцию на амплитудно-фазовой решетке. Пусть ее пропускание описывается комплексной, периодической с периодом  в направлении оси
в направлении оси 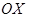 , а в направлении
, а в направлении 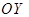 - постоянной функцией
- постоянной функцией  , т.е.
, т.е.

|  (8) (8)
|
Предположим, что на решетку падает световая волна с постоянной амплитудой 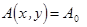 и плоским волновым фронтом в направлении нормали к решетки
и плоским волновым фронтом в направлении нормали к решетки 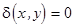 , то распределение поля после решетки будет
, то распределение поля после решетки будет 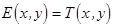 . Если решетка имеет ширину (в направлении оси
. Если решетка имеет ширину (в направлении оси 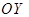 )
)  , а длину
, а длину  , где
, где 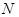 - число элементов решетки (будем считать, что длина решетки в точности равна целому числу элементов), то интеграл (3) и этом случае примет вид
- число элементов решетки (будем считать, что длина решетки в точности равна целому числу элементов), то интеграл (3) и этом случае примет вид
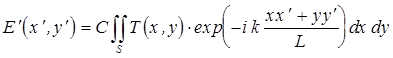 , (9)
, (9)
где 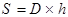 - область, занимаемая решеткой (область интегрирования), а в постоянную
- область, занимаемая решеткой (область интегрирования), а в постоянную 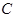 включено значение амплитуды падающего света
включено значение амплитуды падающего света  . Так как
. Так как  не зависит от
не зависит от  , то по
, то по  можно выполнить интегрирование (вынести множитель
можно выполнить интегрирование (вынести множитель  за знак интеграла по
за знак интеграла по 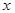 , после чего интеграл по
, после чего интеграл по  вычисляется без труда). Включив результат интегрирования по
вычисляется без труда). Включив результат интегрирования по  в
в 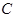 , которая будет зависеть только от
, которая будет зависеть только от  , запишем (9) в виде однократного интеграла
, запишем (9) в виде однократного интеграла
 . (10)
. (10)
Разбивая интервал интегрирования на 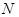 интервалов длиной
интервалов длиной  каждый, заменим (10) суммой
каждый, заменим (10) суммой 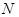 интегралов
интегралов
 (11)
(11)
Делая в каждом  - ом
- ом  интеграле
интеграле
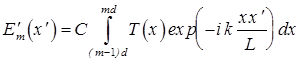 (12)
(12)
замену переменной  , получим
, получим

 ,. (13)
,. (13)
так как  в силу периодичности
в силу периодичности  .
.
После подстановки (13) в (11) все интегралы (они одинаковые) вынесутся за скобки и (11) примет вид
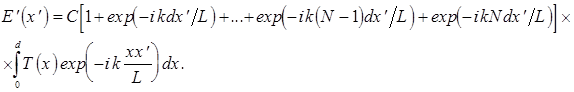 (14)
(14)
Выражение в квадратных скобках представляет собой геометрическую прогрессию из 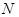 членов, первый из них равен единице, а знаменатель -
членов, первый из них равен единице, а знаменатель - 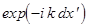 . Суммируя, получим
. Суммируя, получим
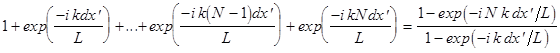 . (15)
. (15)
Так как фиксируется лишь освещенность электромагнитного поля, то для ее определения ее необходимо взять квадрат модуля выражения (11).
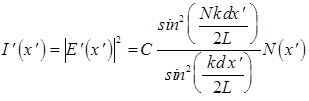 , (16)
, (16)
|
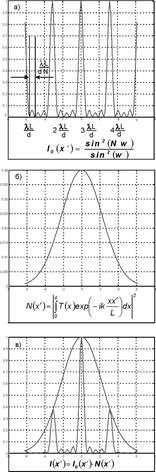
| Рис 2. Распределение освещенности в дифракционной картине от пространственной структуры.
|
где  и учтено, что квадрат модуля выражения (15) есть
и учтено, что квадрат модуля выражения (15) есть  (которое получилось умножением (15) вначале на комплексно сопряженную величину, а затем использована формула Эйлера).
(которое получилось умножением (15) вначале на комплексно сопряженную величину, а затем использована формула Эйлера).
Из (16) следует то, что распределения всех периодических структур имеют общий характер, описываемый множителем перед интегралом, а конкретный вид распределения определяется интегральным выражением 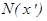 , называемым структурной функцией решетки. Заметим, что
, называемым структурной функцией решетки. Заметим, что 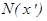 представляет собой распределение освещенностей в дифракционной картине от одного элемента структуры рис (2б). График зависимости
представляет собой распределение освещенностей в дифракционной картине от одного элемента структуры рис (2б). График зависимости  приведен на рис(16). Он может быть получен умножением графика
приведен на рис(16). Он может быть получен умножением графика  на график структурной функции
на график структурной функции 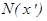 , который является для
, который является для  как бы огибающей. Построим график
как бы огибающей. Построим график  .
.
Запишем это выражение, введя безразмерную переменную 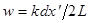 , т.е. будем исследовать зависимость
, т.е. будем исследовать зависимость
 . (17)
. (17)
Данная формула представляет собой отношение двух периодических функций, причем период знаменателя 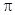 , а период числителя в
, а период числителя в 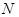 раз меньше, т.е.
раз меньше, т.е.  . Из теории периодических функций, известно, что их отношение также будет периодической функцией с наибольшим у этих функций периодом
. Из теории периодических функций, известно, что их отношение также будет периодической функцией с наибольшим у этих функций периодом  .
.
Знаменатель обращается в нуль при
 (18)
(18)
где  - целое число, однако в этих точках и числитель обращается в нуль, т.е. в этих точках возникает неопределенность типа
- целое число, однако в этих точках и числитель обращается в нуль, т.е. в этих точках возникает неопределенность типа  . Раскрывая ее по правилу Лопиталя, найдем, что значение функции в этих точках равно
. Раскрывая ее по правилу Лопиталя, найдем, что значение функции в этих точках равно  .
.
Так как 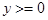 , то минимум функции когда
, то минимум функции когда  , т.е. при
, т.е. при  , т.е. при
, т.е. при
 . (19)
. (19)
Числитель функции осциллирует значительнее чем знаменатель, то можно считать, что  будет иметь также максимумы приблизительно в тех точках, когда
будет иметь также максимумы приблизительно в тех точках, когда 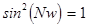 , т.е. при
, т.е. при
 . (20)
. (20)
Значения  в этих точках будут
в этих точках будут  и при больших значениях
и при больших значениях 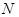 (это можно доказать)
(это можно доказать)  т.е. их величины значительно меньше, чем у максимумов, положения которых определено (18).
т.е. их величины значительно меньше, чем у максимумов, положения которых определено (18).
Таким образом, рассматриваемая функция будет иметь главные максимумы, в точках, определяемых условиями
 , (21.а)
, (21.а)
откуда положения главных максимумов
 . (21.б)
. (21.б)
По аналогии определим положения максимумов  . Они называются побочными (из (20))
. Они называются побочными (из (20))
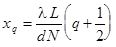 (22)
(22)
и минимумов 
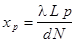 . (23)
. (23)
Из анализа выражений (21) - (23) следует, что между двумя главными максимумами находится  побочных максимума, разделенных
побочных максимума, разделенных  минимумами, так как расстояние между побочными максимумами в
минимумами, так как расстояние между побочными максимумами в 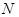 раз меньше, чем между главными. График этой функции показан на рис 2 а.
раз меньше, чем между главными. График этой функции показан на рис 2 а.
Структурная функция, как уже отмечалось, представляет собой дифракционное распределение интенсивности от одного элемента периодической структуры. Это значительно более плавно изменяющаяся функция и ее примерный вид показан на рис 2 б. Наконец, дифракционное распределение от всей структуры показано на рис 2 в и получено как произведение двух верхних графиков.
Из сказанного ясно, что основным параметром, характеризующим дифракционную структуру, является ее пространственный период  , именно от него зависят положения главных максимумов. Все остальные параметры дифракционного распределения играют второстепенную роль. Параметр
, именно от него зависят положения главных максимумов. Все остальные параметры дифракционного распределения играют второстепенную роль. Параметр  носит название постоянной решетки.
носит название постоянной решетки.

|
| Рис 3. Дифракционная решетка (сечение)
|
Рассмотрим плоскую одномерную амплитуднуюдифракционную решетку или, просто дифракционную решетку. Она состоит из ряда прозрачных прямоугольных отверстий шириной 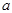 и шириной непрозрачной части
и шириной непрозрачной части  так, что
так, что 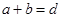 . Согласно (16), влияние этих параметров скажется через структурную функцию решетки, для чего надо вычислить интеграл
. Согласно (16), влияние этих параметров скажется через структурную функцию решетки, для чего надо вычислить интеграл
 , (24)
, (24)
где  - функция пропускания одного элемента решетки.
- функция пропускания одного элемента решетки.
 . (25)
. (25)
В этом случае интеграл примет очень простой вид и его вычисление проводится без труда
|
| Рис 4. Дифракционная картина решетки
|
 . (26)
. (26)
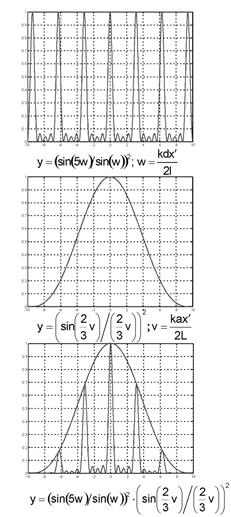
После определения квадрата модуля полученного выражения и подстановки его в (16), распределение освещенности в дифракционной картине примет вид
. (27)
Распределение освещенности от решетки с  показан на рис 4. Так как ширина структурной функции обратно пропорциональна размеру прозрачной части штриха
показан на рис 4. Так как ширина структурной функции обратно пропорциональна размеру прозрачной части штриха 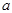 , то решетке присуще некоторое противоречие: при уменьшении
, то решетке присуще некоторое противоречие: при уменьшении 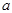 - с одной стороны все большее число главных максимумов имеют достаточно большую амплитуду, а с другой - через решетку проходит меньше света. Это особенно важно при использовании дифракционной решетки в качестве диспергирующего элемента в спектральных приборах - в них используется зависимость положения главных максимумов от
- с одной стороны все большее число главных максимумов имеют достаточно большую амплитуду, а с другой - через решетку проходит меньше света. Это особенно важно при использовании дифракционной решетки в качестве диспергирующего элемента в спектральных приборах - в них используется зависимость положения главных максимумов от 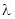 и эта зависимость пропорциональна номеру (порядку) главного максимума. Возможны ситуации, когда минимумы структурной функции совпадают с главными максимумами. Рассмотрим условия их возникновения. Минимумы структурной функции возникают при
и эта зависимость пропорциональна номеру (порядку) главного максимума. Возможны ситуации, когда минимумы структурной функции совпадают с главными максимумами. Рассмотрим условия их возникновения. Минимумы структурной функции возникают при 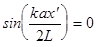 , т.е. при
, т.е. при
 . (28)
. (28)
Сравнивая это выражение с (18), найдем, что это совпадение выполнится при
 . (29)
. (29)
Именно такой случай представлен на рис 4, где третий главный максимум подавлен вторым минимумом структурной функции.

 от главного максимума до максимумов
от главного максимума до максимумов  ,
, 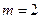 порядков. Для вычисления длины волны используем формулу (2)
порядков. Для вычисления длины волны используем формулу (2) (3)
(3)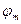 - угол дифракции m-го порядка
- угол дифракции m-го порядка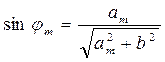
 (4)
(4)
 - ошибка определения b и
- ошибка определения b и  цены деления линеек.
цены деления линеек.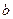 , мм
, мм
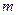
 , нм
, нм
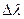 , нм
, нм
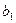 от экрана.
от экрана. от главного максимума до максимума 1-го порядка. 3.Установить решётку на расстоянии
от главного максимума до максимума 1-го порядка. 3.Установить решётку на расстоянии  и измерить расстояние
и измерить расстояние  до максимума 2-го порядка.
до максимума 2-го порядка.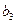 измерить
измерить  для максимума 3-го порядка.
для максимума 3-го порядка. по формуле:
по формуле:
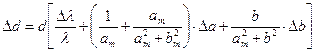

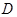 , расстояние от объекта до точки наблюдения
, расстояние от объекта до точки наблюдения  и длина волны излучения
и длина волны излучения 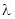 связаны соотношением
связаны соотношением , (1)
, (1) является радиусом первой зоны Френеля. Если выполняется такое условие, то говорят, что наблюдения проводятся в дальней зоне.
является радиусом первой зоны Френеля. Если выполняется такое условие, то говорят, что наблюдения проводятся в дальней зоне.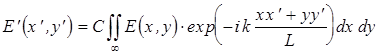 , (2)
, (2)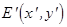 ,
,  - распределения комплексных амплитуд в плоскости наблюдения и в плоскости объекта, где происходит дифракция, соответственно;
- распределения комплексных амплитуд в плоскости наблюдения и в плоскости объекта, где происходит дифракция, соответственно; 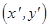 ,
,  - координаты в отмеченных выше плоскостях;
- координаты в отмеченных выше плоскостях; 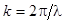 - волновое число;
- волновое число; 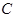 - константа, зависящая от расстояния, влияющая лишь на общую яркость дифракционного распределения, но никак не сказывающейся на его структуре (это так называемая нормировочная постоянная, ее можно положить равной единице и мы в дальнейшем будем ее опускать). В этом выражении предполагается бесконечная область интегрирования, однако на практике эта область фактически конечна: она либо ограничена непрозрачным экраном (или несколькими экранами), либо поле сосредоточено в некоторой области, хотя спадая, простирается до бесконечности (например, по экспоненциальному закону). Площадь этой области
- константа, зависящая от расстояния, влияющая лишь на общую яркость дифракционного распределения, но никак не сказывающейся на его структуре (это так называемая нормировочная постоянная, ее можно положить равной единице и мы в дальнейшем будем ее опускать). В этом выражении предполагается бесконечная область интегрирования, однако на практике эта область фактически конечна: она либо ограничена непрозрачным экраном (или несколькими экранами), либо поле сосредоточено в некоторой области, хотя спадая, простирается до бесконечности (например, по экспоненциальному закону). Площадь этой области 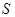 определяет размер объекта, на котором происходит дифракция (
определяет размер объекта, на котором происходит дифракция ( ).
). , (3)
, (3)


 - амплитудное пропускание, определяемое прозрачностью объекта в точке
- амплитудное пропускание, определяемое прозрачностью объекта в точке  - фазовое пропускание, которое в частности связано с функцией профиля одной из поверхностей объекта
- фазовое пропускание, которое в частности связано с функцией профиля одной из поверхностей объекта  (если другая поверхность плоская) соотношением
(если другая поверхность плоская) соотношением , (4)
, (4) - показатель преломления вещества объекта,
- показатель преломления вещества объекта,  , (5)
, (5)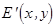 станет
станет , (6)
, (6)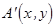 и фаз
и фаз  после объекта будут
после объекта будут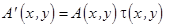 ,
, 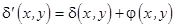 . (7)
. (7) в направлении оси
в направлении оси 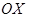 , а в направлении
, а в направлении 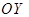 - постоянной функцией
- постоянной функцией  , т.е.
, т.е.
 (8)
(8)
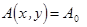 и плоским волновым фронтом в направлении нормали к решетки
и плоским волновым фронтом в направлении нормали к решетки 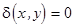 , то распределение поля после решетки будет
, то распределение поля после решетки будет 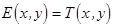 . Если решетка имеет ширину (в направлении оси
. Если решетка имеет ширину (в направлении оси  , а длину
, а длину  , где
, где 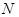 - число элементов решетки (будем считать, что длина решетки в точности равна целому числу элементов), то интеграл (3) и этом случае примет вид
- число элементов решетки (будем считать, что длина решетки в точности равна целому числу элементов), то интеграл (3) и этом случае примет вид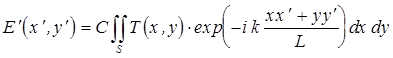 , (9)
, (9)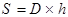 - область, занимаемая решеткой (область интегрирования), а в постоянную
- область, занимаемая решеткой (область интегрирования), а в постоянную  . Так как
. Так как  не зависит от
не зависит от  , то по
, то по  за знак интеграла по
за знак интеграла по 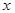 , после чего интеграл по
, после чего интеграл по  , запишем (9) в виде однократного интеграла
, запишем (9) в виде однократного интеграла . (10)
. (10) (11)
(11) - ом
- ом  интеграле
интеграле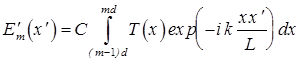 (12)
(12) , получим
, получим
 ,. (13)
,. (13) в силу периодичности
в силу периодичности  .
.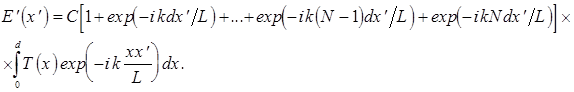 (14)
(14)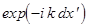 . Суммируя, получим
. Суммируя, получим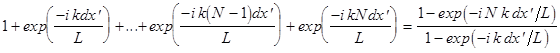 . (15)
. (15)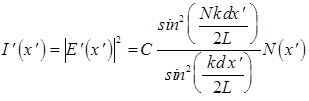 , (16)
, (16)
 и учтено, что квадрат модуля выражения (15) есть
и учтено, что квадрат модуля выражения (15) есть  (которое получилось умножением (15) вначале на комплексно сопряженную величину, а затем использована формула Эйлера).
(которое получилось умножением (15) вначале на комплексно сопряженную величину, а затем использована формула Эйлера).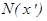 , называемым структурной функцией решетки. Заметим, что
, называемым структурной функцией решетки. Заметим, что  приведен на рис(16). Он может быть получен умножением графика
приведен на рис(16). Он может быть получен умножением графика 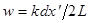 , т.е. будем исследовать зависимость
, т.е. будем исследовать зависимость . (17)
. (17)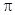 , а период числителя в
, а период числителя в  . Из теории периодических функций, известно, что их отношение также будет периодической функцией с наибольшим у этих функций периодом
. Из теории периодических функций, известно, что их отношение также будет периодической функцией с наибольшим у этих функций периодом  .
. (18)
(18) . Раскрывая ее по правилу Лопиталя, найдем, что значение функции в этих точках равно
. Раскрывая ее по правилу Лопиталя, найдем, что значение функции в этих точках равно  .
.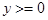 , то минимум функции когда
, то минимум функции когда  , т.е. при
, т.е. при  , т.е. при
, т.е. при . (19)
. (19)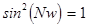 , т.е. при
, т.е. при . (20)
. (20) и при больших значениях
и при больших значениях  т.е. их величины значительно меньше, чем у максимумов, положения которых определено (18).
т.е. их величины значительно меньше, чем у максимумов, положения которых определено (18). , (21.а)
, (21.а) . (21.б)
. (21.б) . Они называются побочными (из (20))
. Они называются побочными (из (20))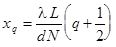 (22)
(22)
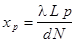 . (23)
. (23) побочных максимума, разделенных
побочных максимума, разделенных  минимумами, так как расстояние между побочными максимумами в
минимумами, так как расстояние между побочными максимумами в 
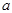 и шириной непрозрачной части
и шириной непрозрачной части  так, что
так, что 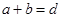 . Согласно (16), влияние этих параметров скажется через структурную функцию решетки, для чего надо вычислить интеграл
. Согласно (16), влияние этих параметров скажется через структурную функцию решетки, для чего надо вычислить интеграл , (24)
, (24) - функция пропускания одного элемента решетки.
- функция пропускания одного элемента решетки. . (25)
. (25)
 . (26)
. (26) показан на рис 4. Так как ширина структурной функции обратно пропорциональна размеру прозрачной части штриха
показан на рис 4. Так как ширина структурной функции обратно пропорциональна размеру прозрачной части штриха 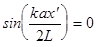 , т.е. при
, т.е. при . (28)
. (28) . (29)
. (29)


