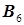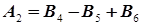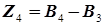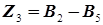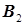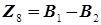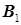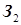С ПОМОЩЬЮ СВЯЗНЫХ ГРАФОВ
Деталь в процессе ее изготовления можно рассматривать как геометрический объект, состоящий из множества поверхностей, связанных между собой конструкторскими и технологическими размерами. Такую структуру целесообразно изучать с использованием теории графов, потому что она дает мощный, простой и доступный инструмент построения моделей и решения задач упорядочения объектов. Граф – геометрическое изображение структуры математической системы G = (V, E) состоящей из непустого множества объектов (рис. 22, а), изображаемых точками V, называемыми вершинами графа (рис. 22, б), связи между которыми показываются множеством линий произвольной конфигурации Е, называемых ребрами графа (рис. 22, в). Для указания направления связи между вершинами графа соответствующее ребро отмечается стрелкой. Ориентированное таким образом ребро называется дугой (рис. 22, д), а граф с ориентированными ребрами - ориентированным графом или орграфом (рис. 22, г).
Если множество вершин графа конечно, то он называется конечным графом. Конечный граф G = (V, E), содержащий p вершин и q ребер, называется (p, q) -графом. Пусть Две вершины Граф можно представить также матрицей смежности. Строки и столбцы этой матрицы соответствуют вершинам графа, а ее Две вершины графа называются связанными, если существует маршрут, соединяющий эти вершины. Граф, любая пара вершин которого связана, называют связным графом. Особый интерес представляют связные графы не имеющие циклов, называемые деревьями. Дерево на множестве Среди различных деревьев выделяются два важных частных случая: последовательное дерево, представляющее собой простую цепь, и звездное дерево, в котором одна из вершин (центр) смежная со всеми остальными вершинами. Ориентированное дерево (дерево с ориентированными ребрами – дугами) называется прадеревом с корнем
Для того чтобы построить дерево, необходимо выбрать какую либо вершину, например вершину Если принять поверхности заготовки или детали за вершины, конструктивные и размерные связи между ними (размеры) за ребра, то чертеж детали и заготовки с конструкторскими размерами и операционные эскизы с технологическими размерами можно представить в виде графов и в частности деревьев. Например, требуется изобразить в виде графа и матрицы смежности конструктивные и размерные связи валика, показанного на рис. 6. Граф для этого примера изображен на рис. 25. На рис. 25 конструктивные связи детали изображены (тонкими линиями) в виде ребер графа, т.к. здесь безразлично, связана, например, конструктивно поверхность 2 с поверхностью 3 или наоборот (они просто связаны между собой). Размеры также проставлены между поверхностями, в этом примере нет приоритета, какая из поверхностей является базой при обработке детали. Поэтому и размерные связи изображены (толстыми линиями) в виде ребер, а не дуг графа. Если же важно будет указать, что одна поверхность является базовой, а положение другой задано относительно ее, то в графе связь между этими поверхностями следует изобразить в виде дуги, исходящей из вершины, отождествляющей первую поверхность и входящей в вершину, отождествляющую вторую поверхность. Матрица смежности данного графа показана на рис. 26.
Рис. 26. Матрица смежности
Дерево с конструкторскими размерами и размерами припусков на обработку называется исходным, а дерево с технологическими размерами и размерами заготовки называется производным. Если на одном рисунке совместить оба эти дерева, то получившийся совмещенный граф представляет собой математическую модель размерных связей технологического процесса механической обработки детали. Этот граф дает полное представление о геометрической структуре технологического процесса и о взаимосвязи конструкторских размеров детали с технологическими размерами, величинами припусков и размерами заготовки. В нем все размерные связи и технологические размерные цепи проявляются в явном виде. Появляется возможность, не прибегая к помощи чертежа, а пользуясь толь совмещенным графом технологического процесса, производить точностной анализ. Любой цикл на совмещенном графе, состоящий из ребер исходного и производного деревьев, образует технологическую размерную цепь, в которой ребро исходного дерева является замыкающим звеном, а ребра производного дерева – составляющими звеньями. В терминах теории графов размерная цепь – это путь, заданный ребрами исходного дерева. Чтобы указать путь, необходимо перечислить ребра, по которым надлежит идти. Если известны длины ребер (размеры, допуски) производного дерева в заданной цепи, то можно найти и длину пути, то есть размер или допуск замыкающего звена. В каждой технологической размерной цепи только одно ребро должно быть ребром исходного дерева (конструкторский размер или допуск), а остальные ребра должны быть ребрами производного дерева, то есть технологическими размерами. Кратчайшим циклом является цикл, состоящий из двух ребер. Ему соответствует двухзвенная размерная цепь, в которой ребро исходного дерева (конструкторский размер) является замыкающим, а ребро производного дерева (технологический размер) – составляющим увеличивающим звеном. Для построения размерного графа технологического процесса необходимы следующие исходные данные: чертеж детали; чертеж заготовки; операционные эскизы выбранного варианта технологического процесса механической обработки детали. Однако, для построения графа удобнее пользоваться предварительно построенной размерной схемой технологического процесса, на которой все исходные данные представлены в систематизированном виде. Порядок построения размерного графа технологического процесса рассмотрим на примере технологического процесса изготовления втулки (рис. 27). Построение графа технологического процесса производится в четыре этапа: Этап 1. Построение производного дерева. Для построения исходного дерева в качестве корня необходимо выбирать вершину (поверхность) к которой на размерной схеме технологического процесса не подходит ни одна стрелка технологического размера. Например, на рис. 8, а такой вершиной является поверхность 9.
Из вершины 9 также выходят две дуги З 2 и В 1, которые подходят, соответственно, к вершинам 6 и 2. Из вершины 6 никаких дуг не выходит, а из вершины 2 выходит дуга В 2 к вершине 8. Из вершины 8 выходят три дуги: В 3 – к вершине 5, В 4 – к вершине 4 и В 5 – к вершине 3. Дуга В 6 соединяет вершину 3 с вершиной 7. Из вершин 4 и 5 никаких дуг не выходит. На этом построение производного дерева заканчивается. Этап 2. Построение исходного дерева. Исходное дерево (рис. 29) строится аналогично, производному дереву.
Так как ребра исходного дерева не ориентированы, то они указывают лишь на то, какие вершины связаны между собой конструкторскими размерами или размерами припусков. В данном случае поверхность 9 связана с поверхностью 8 размером припуска Z 8, а вершина 8 с вершиной (поверхностью) 7 размером припуска Z 7. Поверхность 7 связана с двумя поверхностями: конструкторским размером А 1 с поверхностью 3 и конструкторским размером А 2 с поверхностью 4. Вершина 4 связана с вершиной 5 величиной припуска Z 4. От вершины 5 выходит ребро Z 5 к вершине 6. Поверхность 2 связана с поверхностью 1 размером припуска Z 2.На этом построение исходного дерева заканчивается. Этап 3. Проверка правильности построения деревьев. После построения каждого из деревьев необходимо произвести проверку правильности их построения: число вершин у каждого дерева должно равняться числу поверхностей на размерной схеме технологического процесса; число ребер у каждого дерева должно быть одинаковым и равняться числу вершин без единицы; к каждой вершине производного дерева, кроме корневой, должна подходить только одна стрелка ориентированного ребра (дуги), а к корневой вершине – ни одной дуги; деревья не должны иметь несвязных вершин и циклов. С помощью построенных производного и исходного деревьев появляется возможность определения ошибок в простановке размеров на чертежах заготовки и детали, а также на операционных эскизах. Несвязная вершина на дереве указывает на отсутствие на чертеже или на операционном эскизе необходимых размеров. Цикл на дереве указывает на наличие лишних размеров.
Практически два дерева отдельно не строятся, а необходимо поступать следующим образом: вначале строится производное дерево, а затем на нем же строится исходное дерево, в результате чего совмещение деревьев происходит само собой. При построении деревьев необходимо располагать вершины таким образом, чтобы не произошло пересечение ребер. Совмещенный граф производного и исходного деревьев и будет графом технологического процесса (рис. 30). Любой замкнутый контур совмещенного графа образует размерную цепь, у которой ребро исходного дерева является замыкающим звеном, а ребра производного дерева – составляющими звеньями. Например, на рис. 30 дуги В 1, В 2 и ребро Z 8 образуют замкнутый контур, то есть технологическую размерную цепь, у которой дуги В 1, и В 2 являются составляющими звеньями, а ребро Z 8 – замыкающим звеном. Замкнутый контур, состоящий из дуг В 2, В 3 и ребра Z 3 также образуют размерную цепь, у которой замыкающим звеном является ребро Z 3, а составляющими звеньями – дуги В 2, В 3. Дуга А 2 является замыкающим звеном в размерной цепи, состоящей из звеньев В 4, В 5, В 6 и А 2. В размерной цепи должно быть только одно замыкающее звено, а в технологической размерной цепи им может быть конструкторский размер или величина припуска, поэтому при выявлении размерных цепей по графу необходимо выбирать такие контуры, в которых бы содержалось только по одному ребру исходного дерева, а остальные ребра принадлежали бы производному дереву. Например, на рис. 30 ребра З 2, В 1, В 2, В 4, Z 4 и Z 5 образуют замкнутый контур, но в нем два ребра Z 4 и Z 5, принадлежат исходному дереву, поэтому такой контур не должен использоваться в качестве технологической размерной цепи. В данном случае необходимо рассмотреть два контура, а именно замкнутый контур из ребер В 3, В 4, Z 4 и контур из ребер З 2, В 1, В 2, В 3 и Z 5, каждый из которых представляет собой замкнутую технологическую размерную цепь. В замкнутом контуре, состоящем из ребер В 4, В 5, А 1 и А 2, два ребра (А 1 и А 2) принадлежат исходному дереву, поэтому для расчета необходимо использовать размерную цепь, состоящую из звеньев В 4, В 5, В 6 и А 2, то есть вместо А 1 целесообразно использовать звено В 6. Общее число технологических размерных цепей определяемых с помощью графа должно равняться числу технологических размеров и размеров заготовки на размерной схеме технологического процесса. Одновременно с выявлением технологических размерных цепей необходимо по графу определить также типы составляющих звеньев, а, следовательно, и их знаки в расчетных уравнениях. Определение типов составляющих звеньев цепи производится в результате обхода замкнутого контура для выбранной технологической размерной цепи. Обход начинается от вершины замыкающего звена, которая имеет больший номер, к его вершине, имеющей меньший номер. При этом замыкающему звену всегда в расчетном уравнении размерной цепи присваивается знак минус. Если в направлении обхода следующее ребро размерной цепи будет соединять вершину меньшего порядкового номера с вершиной большего номера, то звену присваивается знак плюс, если же ребро соединяет вершину большего номера с вершиной меньшего номера, то ему в расчетном уравнении присваивается знак минус. Одновременно с определением знаков звеньев размерной цепи составляются расчетные уравнения исходя из условия, что алгебраическая сумма всех звеньев размерной цепи, включая и замыкающее звено, равна нулю. Затем эти уравнения преобразуются в исходные, то есть составленные относительно замыкающего звена. В исходных уравнениях, в правой части, звенья, имеющие знак плюс, являются увеличивающими, а имеющие знак минус – уменьшающими. Выявление и расчет технологических размерных цепей по графу технологического процесса, начинается с двухзвенных цепей, а затем в такой последовательности, чтобы в каждой цепи имелось только одно неизвестное по величине звено, а остальные звенья ее были уже определены в результате расчета предыдущих размерных цепей. Для выполнения этого условия необходимо начинать выявление и расчет размерных цепей в последовательности, обратной выполнению операций и переходов, то есть начинать с последней операции и последнего перехода и заканчивать первым переходом и размером заготовки. Для графа на рис. 30 исходные уравнения сведены в таблицу 1. Таблица 1
Построим граф технологического процесса механической обработки ступенчатого вала (рис. 5), размерная схема которого показана на рис. 12.
Производное и исходное деревья и граф размерных связей технологического процесса показаны на рис. 31. Все технологические размерные цепи, представлены на графе в явном виде как замкнутые контуры, состоящие из ребер исходного и производного деревьев, что существенно облегчает их выявление. Исходные уравнения технологических размерных цепей, выявленных по графу размерных связей технологического процесса показаны в таблице 6. На основании полученных уравнений можно проводить расчеты технологических размерных цепей.
|


 и
и  - соответственно множество вершин и ребер (p, q) - графа. Каждое ребро
- соответственно множество вершин и ребер (p, q) - графа. Каждое ребро  соединяет пару вершин
соединяет пару вершин 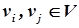 , являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Последовательность ребер, в которой каждые два соседних ребра имеют одну общую вершину и ни какое ребро не встречается более одного раза называется путем в графе.
, являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Последовательность ребер, в которой каждые два соседних ребра имеют одну общую вершину и ни какое ребро не встречается более одного раза называется путем в графе. и
и  графа G = (V, E) называются смежными, если они являются граничными вершинами ребра
графа G = (V, E) называются смежными, если они являются граничными вершинами ребра  . Для неориентированных графов такие пары неупорядочены, так что
. Для неориентированных графов такие пары неупорядочены, так что  , а для ориентированных графов – упорядочены, причем
, а для ориентированных графов – упорядочены, причем  означают, соответственно, начальную и конечную вершины дуги
означают, соответственно, начальную и конечную вершины дуги 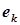 . Петля при вершине
. Петля при вершине  . Ясно, что множество вершин
. Ясно, что множество вершин  вместе с определенным на нем отношением смежности полностью определяет граф.
вместе с определенным на нем отношением смежности полностью определяет граф.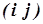 -элемент равен числу кратных ребер, связывающих вершины
-элемент равен числу кратных ребер, связывающих вершины  (или направленных от вершины
(или направленных от вершины 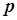 вершин всегда содержит
вершин всегда содержит 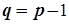 ребер, то есть минимальное количество ребер, необходимое для того, чтобы граф был связным. Действительно, две вершины связываются одним ребром, и для связи каждой последующей вершины с предыдущими требуется ребро, следовательно, для связи
ребер, то есть минимальное количество ребер, необходимое для того, чтобы граф был связным. Действительно, две вершины связываются одним ребром, и для связи каждой последующей вершины с предыдущими требуется ребро, следовательно, для связи  ребер.
ребер. , если существует путь между вершиной
, если существует путь между вершиной 
 , и из нее провести ребра к следующим вершинам
, и из нее провести ребра к следующим вершинам  ,
,  ,
,  (рис. 23), а из них провести ребра в вершинам
(рис. 23), а из них провести ребра в вершинам  ,
,  ,
,  ,
,  ,
,  ,
, 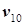 и так далее. Построение дерева может начинаться с любой вершины, поэтому любая вершина может служить корнем дерева.
и так далее. Построение дерева может начинаться с любой вершины, поэтому любая вершина может служить корнем дерева.
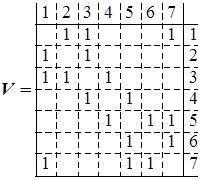

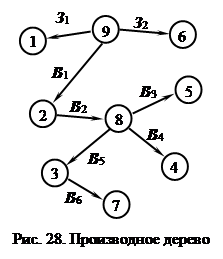 При построении дерева (рис. 28), вершины (поверхности) обозначаются кружочками, с указанием номера поверхности внутри кружочка. Ребра производного дерева являются дугами и изображаются отрезками линий со стрелками на конце показывающими, в какую вершину ребро входит и из какой выходит. Из корня проводятся те дуги, которые выходят из него к другим вершинам. Для данного случая такой дугой будет размер З1, соединяющий вершину 9, являющуюся корнем, с вершиной 1 (рис. 28).
При построении дерева (рис. 28), вершины (поверхности) обозначаются кружочками, с указанием номера поверхности внутри кружочка. Ребра производного дерева являются дугами и изображаются отрезками линий со стрелками на конце показывающими, в какую вершину ребро входит и из какой выходит. Из корня проводятся те дуги, которые выходят из него к другим вершинам. Для данного случая такой дугой будет размер З1, соединяющий вершину 9, являющуюся корнем, с вершиной 1 (рис. 28).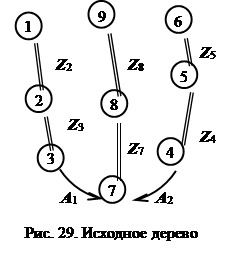 Ребра исходного дерева изображаются в виде скругленных дуг, если они являются конструкторскими размерами, или ненаправленными двойными линиями, если они являются размерами припусков (рис. 29). Ребра исходного дерева не ориентированы, поэтому при его построении в качестве корня можно выбрать любую вершину, то есть любую поверхность на чертеже готовой детали. Порядок расположения вершин на исходном дереве должен быть таким же, как на производном дереве.
Ребра исходного дерева изображаются в виде скругленных дуг, если они являются конструкторскими размерами, или ненаправленными двойными линиями, если они являются размерами припусков (рис. 29). Ребра исходного дерева не ориентированы, поэтому при его построении в качестве корня можно выбрать любую вершину, то есть любую поверхность на чертеже готовой детали. Порядок расположения вершин на исходном дереве должен быть таким же, как на производном дереве. Этап 4. Построение графа технологического процесса. После проверки правильности построения деревьев производится их совмещение, так, чтобы вершины с одинаковыми порядковыми номерами совпадали.
Этап 4. Построение графа технологического процесса. После проверки правильности построения деревьев производится их совмещение, так, чтобы вершины с одинаковыми порядковыми номерами совпадали.