Тема № 5. «Аналитическая геометрия в пространстве: плоскость и прямая, поверхности второго порядка».
Задание 5.1. Даны четыре точки: А (2; n;-4), В (1;3;5), С (n;2;3), D (8; n -1;6), М (1;3;-4), где n – номер варианта. Требуется найти:
1) Уравнение плоскости, проходящей через три точки А, В, С. 3) Уравнение прямой, проходящей через точку D, параллельно плоскости (А, В, С). 4) Расстояние от точки D до плоскости (А, В, С).
Задание 5.2. Дана прямая (l)
1) Написать уравнение плоскости, проходящей через прямую (l) и точку М, 2) Написать уравнение плоскости, проходящей через точку М перпендикулярно прямой (l), 3) Написать уравнение перпендикуляра, опущенного из точки М на прямую (l). Задание 5.3. Заданы плоскость (
1) Вычислить 2) Написать уравнение плоскости, проходящей через прямую (l) перпендикулярно к плоскости ( Задание 5.4. Методом сечений построить график поверхности второго порядка:
Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10 Вариант 11 Вариант 12 Вариант 13 Вариант 14 Вариант 15 Вариант 16 Вариант 17 Вариант 18 Вариант 19 Вариант 20 Вариант 21 Вариант 22 Вариант 23 Вариант 24 Вариант 25 Вариант 26 Вариант 3 Вариант 4 Вариант 5
Литература. 1. Задачник – практикум по математике. Пособие для студентов – заочников. Под редакцией проф. Н. Я. Виленкина. Москва, «Просвещение», 1977. 2. Данко, П.Е. Высшая математика в упражнениях и задачах. Часть 1. В.: 2 ч. [текст] / П.Е. Данко, А.Г. Попов, Т.А. Кожевникова. – М.: ОНИКС, 21 век. Мир и образование, 2008.–368 с. 3. Гордобаева Т.В., Киселева Г.А., Плотникова Н.В., Парыгина С.А., Сенатова И.А. Учебно-методическое пособие «Математика. Часть 2. Линейная алгебра и аналитическая геометрия». 4. Лекции преподавателя.
|

 и точка М (0,1,2), не принадлежащая прямой (проверить). n – номер варианта. Требуется:
и точка М (0,1,2), не принадлежащая прямой (проверить). n – номер варианта. Требуется: и прямая (l)
и прямая (l) 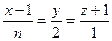 , причем прямая не лежит на плоскости (проверить). Требуется:
, причем прямая не лежит на плоскости (проверить). Требуется: , где
, где  – угол между прямой и плоскостью и координаты точки пересечения прямой и плоскости,
– угол между прямой и плоскостью и координаты точки пересечения прямой и плоскости,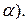
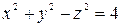 .
.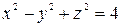 .
. .
.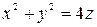 .
. .
.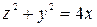 .
.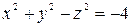
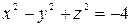 .
. .
. .
. .
.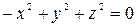 .
. .
.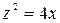 .
.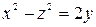 .
.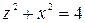 .
. .
. .
.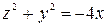 .
. .
. .
.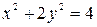 .
. .
. .
. .
. .
. .
. .
. .
.


