Единица длины системы СИ – метр
Поясним, почему в качестве
где ν - число колебаний в секунду (частота излучения), λ - длина волны и с - скорость света. Электроны в атомах, переходя с одной орбиты на другую, излучают (или поглощают) энергию, равную
где h - постоянная Планка, T1 и T2 - энергии разрешенных орбиталей в данном атоме. Одним из следствий теории квантования энергии в атоме является соотношение неопределенности Гайзенберга, утверждающее, что время нахождения электрона в возбужденном состоянии (Δti) и его энергия в этом состоянии (ΔEi) не могут быть одновременно измерены абсолютно точно. Связь эта дается в виде:
или
Другими словами, линия излучаемая или поглощаемая атомами не является монохроматичной и имеет разброс (неопределенность) в энергии, жестко связанный со средним временем нахождения электрона в возбужденном состоянии, называемым временем жизни атома в этом состоянии. Соответственно, контур линии не будет прямоугольным и дается так называемым дисперсионным соотношением:
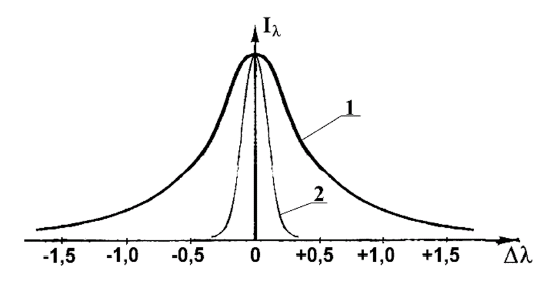
где Iν - интенсивность спектральной линии, ν0 - частота максимума интенсивности линии, Δti - время жизни возбужденного уровня. Это соответствует форме контуры спектральной линии, показанной на рис. 2.1
Индексом Кроме естественного затухания излучения на ширину контура монохроматичной линии в спектре атома влияют: уширения столкновениями с собственными атомами; уширения столкновениями с посторонними атомами; уширение вследствие эффекта Допплера; штарковское уширение. Механизмы столкновительных уширений аналогичны таковым для естественного уширения, т. к. причиной явления является уменьшение времени жизни атома в возбужденном состоянии. Согласно соотношению неопределенности Гайзенберга уменьшение времени жизни Δti приведет к размытию уровня энергии, т. е. увеличению ΔE. Аналитическая зависимость интенсивности будет квазидисперсионная (2.18) где вместо естественного времени жизни уровня Δt нужно подставлять сумму естественного и столкновительного времен жизни атома в возбужденном состоянии
где γ'ст - постоянная затухания излучения вследствие столкновений с собственным газом; γ''ст - постоянная затухания излучения в следствии столкновений с посторонним газом. Механизм допплеровского уширения связан с эффектом изменения частоты излучения, а следовательно и длины волны в зависимости оттого с какой скоростью и в каком направлении двигается излучающий объект. Для спектральной линии атома зависимость распределения интенсивности от длины волны дается выражением:
где ΔνD - допплеровская ширина линии, равная
где Т - температура; μ - молекулярный или атомный вес излучающих частиц; R - газовая постоянная. Штарковское уширение обусловлено изменениями энергии верхнего уровня при наличии сильных электромагнитных полей. Поскольку здесь не стоит проблема детального анализа всевозможных вариантов уширения спектральных линий, ограничимся только упоминанием о таком механизме. В метрологической практике ограничиваются дисперсионным и допплеровским механизмом уширения, т. к. в реальных источниках света можно считать эти факторы преобладающими. Суммарный контур линии с учетом столкновительного и допплеровского уширений в специальной литературе называют фойхтовским. Зависимость интенсивности от длины волны вблизи максимума линии дается выражением:
где у - относительная координата, равная В эталонных измерениях для повышения точности очень важно иметь как можно более узкую (более монохроматичную) линию. Очевидно, что чем выше Перечисленные требования обусловили выбор источников света для эталонов длины на первыхэтапах внедрения системы СИ в измерения. Так, первоначально в эталоне длины использовалась кадмиевая лампа, а в дальнейшем ее заменили на криптоновый источник света, который можно было охлаждать до температуры жидкого азота, уменьшая тем самым допплеровское уширение линий. Большой прогресс в повышении степени монохроматичности источников света для эталона длины был достигнут после открытия в 1962 г. и внедрения в дальнейшем в измерительную технику газоразрядных лазеров. Среди специфических свойств лазерного излучения для
Последние достижения измерительной техники в создании эталона метра состоят в том, что внутрь резонатора лазера помещают кювету (ячейку) с парами какого-либо чистого вещества, например метана или иода. Такое вещество должно иметь линии поглощения на частотах близких к частоте генерации лазера. Поскольку в резонаторе такого лазера часть излучения поглощается, происходит срыв генерации, и на фоне линии лазерного излучения наблюдается провал, называемый провалом Лэмба. Далее электронными системами автоматической подстройки частоты вырабатывается сигнал, возвращающий частоту лазера в прежнее значение. Такими приемами удается уменьшить нестабильность частоты лазера. Для создания эталонов
где n - показатель преломления среды; I - геометрическая длина пути.
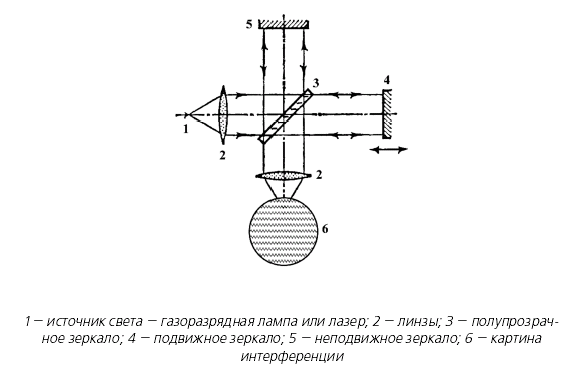
Условие максимума интерференционной картины в интерферометре Майкельсона имеет вид:
условие минимума
Если в приборе, собранном по схеме рис. 2.3 Различные усовершенствования, внесенные в эталон длины, особенно с использованием лазеров, привели к необходимости перейти на новое определение метра, которое было принято в 1983 г. Основными нововведениями были: Переход от криптоновой лампы к лазерному излучению в источнике света на эталонных установках. Использование в качестве основного постулата постоянство скорости света в любой системе отсчета. Объединение в одном эталоне воспроизведения размера трех физических величин: длины, времени и частоты. Использование в эталоне источников света на пяти различных длинах волн. Согласно новому определению метра основной единицей длины системы единиц СИ является длина, равная расстоянию, проходимому светом за 1/с долю секунды. Учитывая, что скорость света, как указывалось выше, равна с = 2,997925 • 108 м/с этот промежуток времени равен t = 3,33564 • 10-9 с. Частоты, на которых было предложено реализовать эталон метра, приведены в табл. 2.2. В первой графе таблицы указан тип лазера, т. е. рабочее вещество, и тип наполнения поглощающей ячейки. Таблица 2.2. Параметры лазерных установок, используемых
При воспроизведении единицы длины на интерферометре следует учитывать, что длины волн источников излучения даны для вакуума. В воздухе необходимо учитывать показатель преломления воздуха, в результате влияния которого длина волны в воздухе равна
где n - показатель преломления. Это означает, что в комплект эталонного комплекса для воспроизведения метра должен входить Прежде чем перейти к проблемам воспроизведения единиц частоты и времени на объединенном эталоне единиц механических величин системы СИ, рассмотрим эволюцию в создании и определении эталона времени. 2.5. Единица времени системы СИ - секунда Исторические аспекты проблемы измерения времени с давних пор связывались с движением Земли вокруг своей оси и с движением Земли вокруг Солнца. Древние астрономы определяли единицу времени как часть дня, т. е. время от восхода до заката Солнца разбивалось на 12 частей (час), затем на 60 частей (минута) и еще на 60 частей (секунда). Но ось вращения Земли наклонена на 23,5° к нормали к плоскости орбиты, поэтому на разных широтах и в разное время года В дальнейшем единицу времени стали связывать с продолжительностью суток, которые уже разбивались на время t = 24×60×60 = 86400 секунд. Было установлено также, что продолжительность суток в разное время года разная, поскольку Земля движется вокруг Солнца по эллиптической орбите. Это приводит к тому, что длительность суток в июне на 16 с отличается от длительности суток в декабре. По этой причине единицу времени привязывали либо к звездным суткам, либо к солнечным. Поскольку на протяжении одного года наблюдается п солнечных суток и (n+1) звездных суток, то единицы времени, определенные по суткам днем и ночью несколько отличались. Разница звездных и солнечных суток составляет около 4-х минут. Следует также учитывать, что год, т. е. период обращения Земли вокруг Солнца, тоже может определяться по-разному. В метрологической практике использовались три различные определения года:
1 год троп. = 365, 24220 средних солнечных суток. Продолжительность тропического года превышает целое число дней (365) примерно на 1/4 суток. Поэтому каждый четвертый год становится високосным, т. е. к нему добавляют 366-й день. Кроме того, по международным соглашениям некоторые года дополнительно удлиняются. Например, високосный год 1972 был на 2 секунды длиннее других високосных лет.
1 сидерический год = 365,25636 средних солнечных суток.
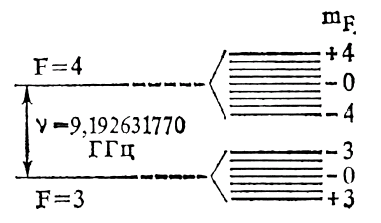
1 аномалистический год = 365,25946 средних солнечных суток. Учитывая всевозможные причины непостоянства определения единицы времени на основе измерений параметров движения Земли, Международным бюро по мерам и весам в 1956 г. было принято определение так называемой 1 секунда = (1/31556925,9747) тропического года 1900, при этом началом отсчета является 31 декабря 1899 г. в 12 часов, а концом отсчета является 0-е января 1900 г. в 12 часов. Это время обозначалось как ЕТ. Эфемеридная секунда и отметки точного времени, связанные с вращением Земли, служили основной единицей практически во всех системах единиц до тех пор, пока не встала проблема определения единицы времени с относительной погрешностью не хуже 10-10. Кроме того, нужен был способ воспроизведения единицы времени, который позволял бы это сделать за промежуток времени, меньший, чем год. По этой причине XII Генеральная конференция по мерам и весам поручила Международному комитету по мерам и весам установить некую молекулярную или атомную частоту, которая должна с 1967 г. стать определением единицы времени в системе СИ. Это означало переход от воспроизведения единицы времени к воспроизведению частоты какого-либо стабильного во времени периодического процесса. В результате международных обсуждений и согласований в 1967 г. было принято следующее определение единицы времени. Единица времени - 1 секунда - равна продолжительности 9,192 631770 ×109 колебаний излучения при квантовом переходе между линиями сверхтонкой структуры атома цезия 133Cs, соответствующих переходу [F = 4; mF = 0] [F = 3; mF = 0] основного состояния 2S1/2. Для того чтобы воспринимать сознательно это определение, поясним смысл обозначений уровней энергии, принятых в спектроскопии. Мы ранее указывали, что уровни энергии в атоме имеют дискретные значения. Их величина зависит от Добавление к орбитальному моменту спина электрона приводит к мульти плотному расщеплению уровня с одинаковыми орбитальными моментами на несколько подуровней. Соответственно, Расщепление уровней по полному моменту приводит к появлению так называемого тонкого расщепления. Если теперь к этому моменту добавить момент ядра I, то каждый уровень тонкой структуры расщепится дополнительно, поскольку момент ядра может либо добавиться к моменту J, либо от него отнимется. В результате образуется полный момент, обозначаемый в спектроскопии буквой F. Таким образом, обозначения уровня атома цезия в определении единицы времени указывает на конкретные подуровни сверхтонкой структуры атома цезия. Для них полные моменты F равны 4 и 3, это подуровни основного состояния с числом L = 0, числом S = 1/2, числом J = 1/2. Дополнительные сведения о числе mF относятся к изменению энергии подуровней сверхтонкой структуры в магнитном поле. Выбор в качестве рабочих уровней компонентов сmF = 0 означает, что при наличии магнитного поля нужно выбирать не смещающиеся компоненты. Смысл данного определения единицы времени состоит в том, что расстояние между подуровнями, указанными в определении составляет частоту ν0 = 9,192 631 770 ГГц. Если на ячейку или атомный пучок, содержащие свободные атомы цезия воздействовать электромагнитным полем с частотой ν0, то будет наблюдаться поглощение энергии поля за счет переходов атомов из состояния с F = 3 в состояние с F = 4 в соответствии с диаграммой рис. 2.4
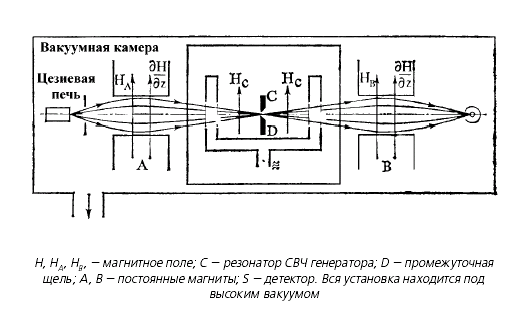
Принцип действия установки для наблюдения резонанса в цезиевом пучке и воспроизведения единицы частоты - Герца - состоял в следующем: В специальном нагревателе испарялся металлический цезий и его атомный пучок распространялся через диафрагмы в вакуумную камеру. На пути пучок попадал в магнитное неоднородное поле, в котором он расширялся и фокусировался на промежуточной щели D. Щель D помещалась внутрь резонатора СВЧ, на который подавался переменный сигнал, близкий к 9,1926 ГГц. За резонатором располагалась еще одна система магнитов, которая фокусировала атомный пучок на детекторе. Изменяя плавно частоту подводимой к резонатору энергии, добивались резкого сигнала с детектора, соответствующего частоте резонанса в цезии. Именно эта частота и соответствовала 9,192631770 • 109 Гц, и зафиксировав ее точно, можно было воспроизвести единицу времени, т. к. t = 1/ν. Сопоставление диапазона длин волн и частот, воспроизводимых на эталоне метра и на эталоне Герца, показывает, что оптические измерения на длине волн 0,6 мкм и радиочастотные измерения отличаются по частоте на четыре порядка: - 1014 Гц для оптического диапазона и - 1010 Гц для радиочастотного. По этой причине при объединении эталонов метра. Герца и секунды кроме установок с интерферометром и с цезиевыми часами необходимо было создать специальный измерительный комплекс, позволяющий сопоставить без потери точности оптические и радиочастотные измерения. Этот комплекс в метрологии получил название «радиочастотный мост». Принцип, положенный в его основу, состоит в том, что умножение частоты колебаний какого-либо процесса может быть реализовано практически без потери точности. Появляется возможность последовательным удвоением, учетверением и т.д. частоты, воспроизведенной на цезиевых часах, вплотную подойти к частотам оптического диапазона - 1014 Гц. В этом случае можно сличить непосредственно параметры электромагнитных колебаний эталона метра и цезиевых часов. Реализация эталона метра, эталона
|

 Метр по определению равен длине 1 650 763,73 длины волны в вакууме излучения, соответствующего переходу между уровнями 2p10-5d5 атома криптона 86 (86Kr). Это определение было принято в 1960 г. В 1927 г. определение было несколько иным, так как в качестве эталона-свидетеля была утверждена длина волны излучения кадмия 114 с длиной волны λ = 0,64402 мкм.
Метр по определению равен длине 1 650 763,73 длины волны в вакууме излучения, соответствующего переходу между уровнями 2p10-5d5 атома криптона 86 (86Kr). Это определение было принято в 1960 г. В 1927 г. определение было несколько иным, так как в качестве эталона-свидетеля была утверждена длина волны излучения кадмия 114 с длиной волны λ = 0,64402 мкм.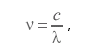 (2.15)
(2.15)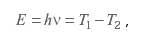 (2.16)
(2.16)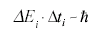
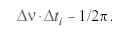 (2.17)
(2.17)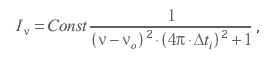 (2.18)
(2.18) .
.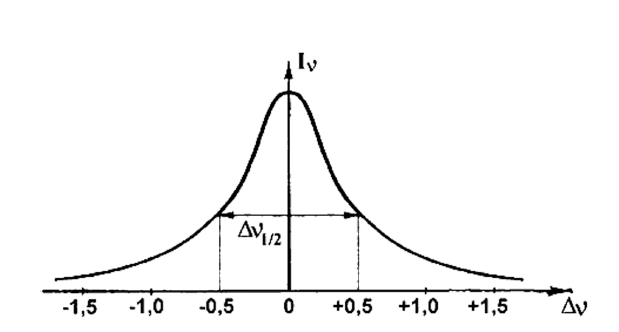
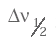 обозначена так называемая естественная ширина линии, т. е. ширина профиля в единицах ν на половине максимального значения.
обозначена так называемая естественная ширина линии, т. е. ширина профиля в единицах ν на половине максимального значения.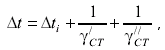 (2.19)
(2.19)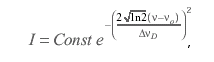 (2.20)
(2.20)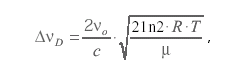 (2.21)
(2.21)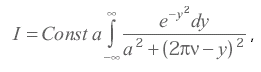 (2.22)
(2.22)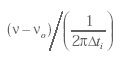 и а - параметр Фойхта, равный
и а - параметр Фойхта, равный 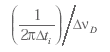 .
.
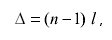
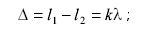 (2.23)
(2.23)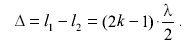 (2.24)
(2.24)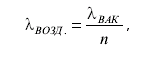
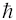 , мультиплетность равна 2. Мультиплетность равна (2J +1), т. е. орбитальный полный момент равен 1/2
, мультиплетность равна 2. Мультиплетность равна (2J +1), т. е. орбитальный полный момент равен 1/2