Формулы размерности
Если с изменением Простейший пример: размерность площади или объема для тех систем единиц, где основной является единица длины. Размерность площади равна двум, размерность объема - трем, т. к.
В более сложных случаях, если единица некоторой величины А имеет размерность р, q и r относительно единиц длины, массы и времени, то формула размерности записывается в виде:
где символы L, М и Т представляют собой обобщенные обозначения единиц длины, массы и силы без конкретного указания размера единиц. Это означает, что если каждую из основных единиц увеличить в 10 раз, то производная единица увеличивается в10pqr раз. Может оказаться, что размер производной единицы не зависит ни от одной из основных единиц. В этом случае говорят, что производная единица безразмерна или обладает нулевой размерностью. При любом выборе основных единиц При образовании формул размерности пользоваться следующими теоремами: Теорема 1. Если числовое значение величины С равно произведению числовых значений величин А и В, то размерность С равна произведению размерностей А и В, т. е.
Теорема 2. Если числовое значение величины С равно отношению числовых значений А и В, то размерность С равна отношению размерностей А и В, т. е.
Теорема 3. Если числовое значение величины С равно степени n числового значения величины А, то размерность С равна степени n размерности А, т. е.
Доказательства этих теорем очень просты, что можно проиллюстрировать доказательством первой из них. Пусть числовое значение С равно произведению числовых значений А и В. При измерении их единицами c1, a1 и b1 имеем
где C1 = С/c1; A1 = А/a1; в, = в/b1. Соответственно при измерении техже величин единицами c2, a2 и b2
где C2 = С/c2; A2 = А/a2; B2 = В/b2. Из сопоставления С, А и В, выраженных разными единицами, получаем:
Если теперь
и
то
что и требовалось доказать. Аналогично нетрудно доказать и другие две теоремы. Важно отметить, что размерность не зависит от наличия или отсутствия в построении производной единицы постоянных безразмерных множителей или безразмерных величин. Это означает, например, что размерность площади квадрата
и площади круга
будут одинаковыми, поскольку коэффициент В заключение рассмотрения понятий размерности рассмотрим, какие изменения в формулах размерности произойдут при разном выборе основных единиц. Очевидно, что в этом случае в формулах размерности будут стоять совсем другие выражения, поскольку связь производных единиц, например в механике, существенно изменится при замене основной единицы массы на основную единицу силы. Например, обозначая размерность основной единицы системы МКГСС-силы символом F получим размерность массы:
Размерность энергии в системе МКГСС будет
Из этого выражения сразу становится понятной привлекательность системы МКГСС для механических расчетов, поскольку энергия столь просто за висит от основных единиц - силы и длины. В заключение раздела, посвященному обзору различных систем единиц, упомянем, что размерность производных единиц не зависит от определения размера производной единицы. Например, если выражать площади плоских фигур в квадратных метрах, когда единицей площади выбирается площадь квадрата со стороной равной единице длины, а затем выразить ту же площадь в «круглых» метрах, т. е. единицу площади определить как площадь круга с диаметром, равным единице длины, то размерность площади при таком переопределении не изменится и будет равна
|

 Формулой размерности называется математическое выражение, показывающее, во сколько раз изменится производная единица при определенных изменениях основных единиц. Для ознакомления с построением формул размерности полезно вначале рассмотреть случай, когда различные системы используют одни и те же основные величины и одни и те же определяющие соотношения. Такими системами, например, являются системы СГС и СИ, в которых для механических величин основными выбраны масса, длина и время. Эти системы отличаются только размером основных механических единиц.
Формулой размерности называется математическое выражение, показывающее, во сколько раз изменится производная единица при определенных изменениях основных единиц. Для ознакомления с построением формул размерности полезно вначале рассмотреть случай, когда различные системы используют одни и те же основные величины и одни и те же определяющие соотношения. Такими системами, например, являются системы СГС и СИ, в которых для механических величин основными выбраны масса, длина и время. Эти системы отличаются только размером основных механических единиц.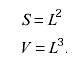 (2.1)
(2.1)
 (2.2)
(2.2)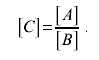 (2.3)
(2.3) (2.4)
(2.4)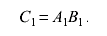 (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8)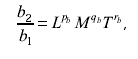 (2.9)
(2.9)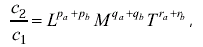 (2.10)
(2.10) (2.11)
(2.11)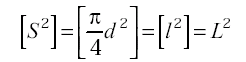 (2.12)
(2.12)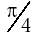 не зависит от размера основных единиц.
не зависит от размера основных единиц. (2.13)
(2.13)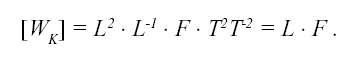 (2.14)
(2.14)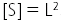 .
.


