Алгоритмы распознавания состояния объекта по экспериментальным данным
Существует несколько методов распознание данных. Далее приведены основные методы распознавания данных. Основы статистической теории распознавания Математически постановка задачи распознавания двух объектов
Располагая этой априорной информацией об объектах, необходимо обосновать правило принятия решения, если получена выборка измерений признаков распознавания. Показателем эффективности распознавания может служить математическое ожидание стоимости принятия ошибочных решений. В рассматриваемом случае возможны два ошибочных решения: 1) принять решение «объект 2) принять решение «объект
Выделим в гиперпространстве признаков
т.е. вероятность того, что в область
Так как вероятность ошибки
Условие минимума математического ожидания стоимости ошибок при принятии решения "объект
Отношение условных многомерных законов распределения называется функцией отношения правдоподобия. Поэтому решающее правило распознавания объекта
и сравнить его с порогом
Логарифм отношения правдоподобия может оказаться очень сложной функцией. Представим ее в виде ряда Тейлора и ограничимся несколькими членами. Предположим, что известны математические ожидания признаков распознавания для объектов
Здесь Запишем ряд Тейлора с тремя членами окрестности вектора
В этом выражении первая производная есть вектор-строка (градиент), вторая производная– матрица Гесса
Если выполнить все операции над векторами и матрицами, то логарифм отношения правдоподобия приближенно можно представить в виде ограниченного ряда Колмогорова-Габора
где коэффициенты Как правило, многомерные законы распределения вероятностей признаков распознавания неизвестны, однако могут быть получены их измерения для некоторого множества объектов класса
Решающее правило распознавания на основе оценок параметров законов распределения
Предположим, что по результатам специально проведенного эксперимента для объектов класса Таблица 2.3.1
Если теоретические законы распределения известны, то их параметры можно оценить по данным табл. 2.3.1. Первичная обработка табличных данных включает оценку математических ожиданий и дисперсий признаков распознавания и коэффициентов корреляции
По результатам первичной обработки можно дать предварительную (качественную) оценку информативности признаков распознавания, выделив коррелированные (зависимые) признаки и признаки с близкими оценками математических ожиданий и дисперсий. Если их исключить из рассмотрения, то по оставшимся признакам можно сформировать функцию отношения правдоподобия и построить решающее правило распознавания. Из рассмотрения на первый взгляд простой задачи распознавания можно сделать важный практический вывод: аналитические возможности исследования эффективности решающих правил распознавания, построенных по экспериментальным данным, весьма ограниченны, особенно при небольших выборках исходных измерений. Построение решающих правил методом группового учета аргументов Рассмотрим задачу распознавания двух объектов Таблица 2.3.2 Исходные данные
По данным таблицы можно было бы восстановить многомерные законы распределения
и записать решающее правило распознавания объекта
Однако восстановление многомерных законов, особенно при небольших выборках– задача сложная. А.Г. Ивахненко предложил метод построения решающих правил распознавания без восстановления законов распределения, получивший название метода группового учета аргументов. Приведем исходные данные к одному масштабу измерений путем их нормировки. Определим по каждому столбцу общие средние значения и выборочные дисперсии
Нормированные данные рассчитаем по формулам
Неизвестный логарифм отношения правдоподобия
представим в виде ряда Колмогорова-Габора. Ряд Колмогорова-Габора – это конечный ряд Тейлора степени
Здесь число неизвестных коэффициентов равно 5, при
если
если Можно составить систему уравнений вида
и решить её относительно неизвестных коэффициентов ряда Колмогорова-Габора Рассмотрим задачу формирования решающей функции на примере четырех параметров
Запишем, используя нормированные данные таблиц
Эти переопределённые системы нормальных уравнений легко решаются. Просуммируем первое по
где Умножив исходные уравнения на
где Третье уравнение запишется в виде:
где Четвертое уравнение сформируем после умножения исходных уравнений на
где Решив систему полученных четырех линейных уравнений, будем иметь значения коэффициентов и оценку первого полинома
Совершенно аналогично определяются коэффициенты второго полинома. Его оценку запишем в виде
Подставив в (2.3.70) и (2.3.71) данные из таблиц исходных нормированных измерений Таблица 2.3.3 Промежуточные данные
Сформируем теперь третий полином Колмогорова-Габора относительно
и оценим его коэффициенты, используя таблицу промежуточных данных
Если теперь вместо
где Решающее правило распознавания объекта
Таким образом, группировка аргументов парами позволяет оценивать неизвестные коэффициенты полиномов при сравнительно небольших выборках измерений, решая однотипные системы линейных уравнений четвертого порядка. Естественным является вопрос о том, как выбирать пары измерений, почему
Вероятности ошибок распознавания можно оценить по экспериментальным данным, используя законы распределения, восстановленные методом сглаженных дельта-функций. В рассматриваемом случае возможны шесть начальных полиномов Колмогорова-Габора: Первая таблица промежуточных данных
Каждому полиному
Для оценки вероятностей воспользуемся восстановленными непосредственно по экспериментальным данным функциями распределения
В результате получим формулы для оценки
Аналогичные формулы записываются для двух других пар аргументов Таблица эффективностей
Прежде чем анализировать эти данные эффективности, проведем теоретическое исследование связей между вероятностями распознавания по каждому из параметров Предположим, что для распознавания используются два параметра:
где Если
Из анализа (4.3.10) можно сделать следующие выводы: 1) если 2) если Теперь вернемся к анализу таблицы эффективности: очевидно, что необходимо отбирать пары с наибольшей эффективностью с несовпадающими индексами. Пары с малой эффективностью имеет смысл исключать с рассмотрения
где Вероятность распознавания по двум параметрам
Рассмотрим числитель под знаком интеграла вероятности. Подкоренное выражение преобразуем к виду:
Так как ошибки оценивания
Если ошибки оценивания параметров нормальные независимые случайные величины с нулевым математическим ожиданием и дисперсией
где Закон распределения
Вероятность выполнения условия (4.3.12) равна
где Известен табличный интеграл
Для определения вероятности
где При больших значениях аргумента функция Бесселя
Следовательно, приближенно вероятность
Вероятность Если после первого отбора остается больше двух пар параметров, например,
Важным достоинством метода группового учёта аргументов является то, что на каждом этапе отбора используются одни и те же алгоритмы. При оценке эффективности алгоритмов распознавания необходимо иметь ввиду следующее обстоятельство. Исходные данные и промежуточные результаты используются дважды: 1) для оценки неизвестных коэффициентов рядов Колмогорова-Габора; 2) для оценки вероятностей распознавания. Как показали исследования, такие оценки завышены (занижены вероятности ошибок). Хотя это мало сказывается на правильности отбора пар признаков, но если исходные выборки данных большого размера (100 и более), то их следует разделить на две группы: 1) обучающие, используемые для оценки коэффициентов полиномов; 2) проверочные, используемые для оценки вероятностей и отбора параметров. Для обучения отбирается примерно 2/3 измерений, для контроля - 1/3. Гистограммный метод распознавания Предположим, что контролируемый объект может находится в двух состояниях и известны выборки измерений, полученные при состоянии
Заменим в (4.4.1)
и определим его логарифм
Для распознавания состояния объекта необходимо по измеренной выборке
Дисперсию
|

 и
и 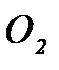 , измеряемые признаки которых являются случайными векторами
, измеряемые признаки которых являются случайными векторами 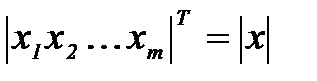 , формулируется следующим образом. Известно, что частоты появления объектов характеризуются вероятностями
, формулируется следующим образом. Известно, что частоты появления объектов характеризуются вероятностями  и
и  , и признаки описываются условными законами распределения:
, и признаки описываются условными законами распределения: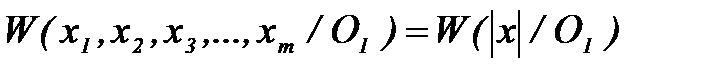 , (2.3.1)
, (2.3.1) . (2.3.2)
. (2.3.2) », если в действительности измерения признаков
», если в действительности измерения признаков 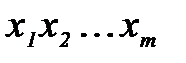 получены от объекта
получены от объекта  .
. », если предъявлен к распознаванию объект
», если предъявлен к распознаванию объект  . Эти события являются случайными и описываются вероятностями
. Эти события являются случайными и описываются вероятностями  и
и  . Если стоимости ошибок обозначить
. Если стоимости ошибок обозначить  и
и 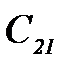 , то их математическое ожидание можно вычислить по формуле
, то их математическое ожидание можно вычислить по формуле . (2.3.3)
. (2.3.3) область
область  , точки которой принадлежат измерениям объекта
, точки которой принадлежат измерениям объекта  . Тогда вероятность правильного распознавания объекта
. Тогда вероятность правильного распознавания объекта  равна
равна (2.3.4)
(2.3.4) попадут измерения, характеризующие объект
попадут измерения, характеризующие объект  , то это будет ошибочное решение, вероятность которого равна
, то это будет ошибочное решение, вероятность которого равна (2.3.5)
(2.3.5) , то, подставив в (2.3.3) выражение для
, то, подставив в (2.3.3) выражение для  и
и  , получим после несложных преобразований
, получим после несложных преобразований (2.3.6)
(2.3.6) " очевидно из анализа выражения (2.3.6): функция в квадратных скобках должна быть больше нуля
" очевидно из анализа выражения (2.3.6): функция в квадратных скобках должна быть больше нуля . (2.3.7)
. (2.3.7)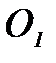 формулируется следующим образом: по выборке измерений
формулируется следующим образом: по выборке измерений  необходимо вычислить отношение правдоподобия
необходимо вычислить отношение правдоподобия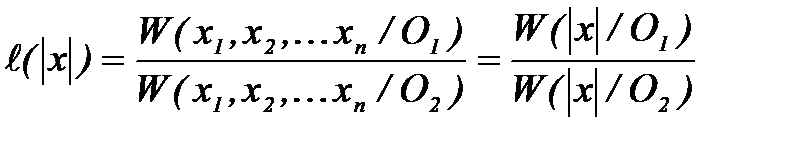 (2.3.8)
(2.3.8) ; если
; если  , то принять решение "объект
, то принять решение "объект  ", если
", если  , то принять решение "объект
, то принять решение "объект  ". В ряде случаев удобно вычислить не отношение правдоподобия, а его логарифм:
". В ряде случаев удобно вычислить не отношение правдоподобия, а его логарифм:  . Тогда решающее правило запишется в виде неравенства
. Тогда решающее правило запишется в виде неравенства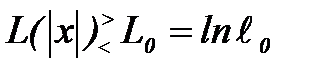 . (2.3.9)
. (2.3.9) и
и 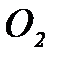 . Определим средний вектор признаков
. Определим средний вектор признаков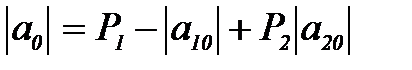 . (2.3.10)
. (2.3.10)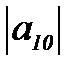 ,
,  ,
,  ,
,  и – математические ожидания измерений и вероятности появления признаков.
и – математические ожидания измерений и вероятности появления признаков.
 . (2.3.11)
. (2.3.11) , (2.3.12)
, (2.3.12) . (2.3.13)
. (2.3.13) , (2.3.14)
, (2.3.14) ,
,  ,
,  , определяются значениями первых и вторых частных произведений логарифмической функции правдоподобия в точках
, определяются значениями первых и вторых частных произведений логарифмической функции правдоподобия в точках 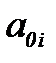 .
. и для объектов класса
и для объектов класса  . Задача состоит в том, что по этим данным построить решающее правило, т.е. алгоритм обработки измерений.
. Задача состоит в том, что по этим данным построить решающее правило, т.е. алгоритм обработки измерений.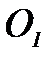 и объектов класса
и объектов класса  получены измерения вектора признаков распознавания и результаты эксперимента сведены в таблицу 2.3.1
получены измерения вектора признаков распознавания и результаты эксперимента сведены в таблицу 2.3.1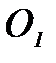




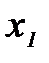
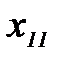

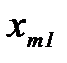









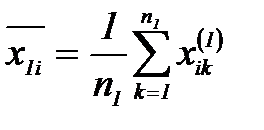 , (2.3.15)
, (2.3.15) , (2.3.16)
, (2.3.16) , (2.3.17)
, (2.3.17) , (2.3.18)
, (2.3.18) , (2.3.19)
, (2.3.19) . (2.3.20)
. (2.3.20)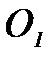 и
и  по измерениям вектора параметров
по измерениям вектора параметров 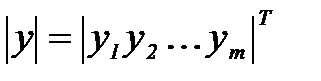 . Параметры могут иметь различную физическую природу и размерность, их законы распознавания неизвестны, но заданы измерения параметров в виде таблиц классифицированных данных
. Параметры могут иметь различную физическую природу и размерность, их законы распознавания неизвестны, но заданы измерения параметров в виде таблиц классифицированных данных 



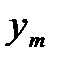






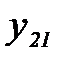




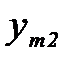






 и
и 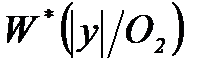 , образовать отношение правдоподобия
, образовать отношение правдоподобия (2.3.21)
(2.3.21) . (2.3.22)
. (2.3.22) . (2.3.23)
. (2.3.23) (2.3.24)
(2.3.24)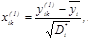 (2.3.55)
(2.3.55) (2.3.56) и составим таблицы
(2.3.56) и составим таблицы 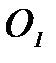 и
и  нормированных исходных данных.
нормированных исходных данных. (2.3.27)
(2.3.27) . Например, при
. Например, при  это полином вида
это полином вида (2.3.28)
(2.3.28) их 20, при
их 20, при  их 75. Коэффициенты ряда модно определить по экспериментальным данным следующим образом. В соответствии с решающим правилом
их 75. Коэффициенты ряда модно определить по экспериментальным данным следующим образом. В соответствии с решающим правилом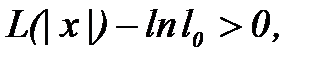 (2.3.29)
(2.3.29)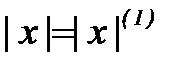 , т.е. измерения принадлежат объектам класса
, т.е. измерения принадлежат объектам класса 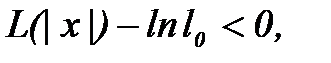 (2.3.30)
(2.3.30)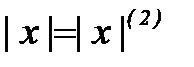 .
. (2.3.31)
(2.3.31) . Однако на практике возникают серьезные трудности из-за большой размерности уравнений, для решения которых требуются выборки больших размеров. А.Г. Ивахненко предложил метод последовательного иерархического формирования решающего правила на основе частных полиномов Колмогорова-Габора второго порядка. В задачах распознавания эффективность решающих правил зависит от различий законов распределения параметров
. Однако на практике возникают серьезные трудности из-за большой размерности уравнений, для решения которых требуются выборки больших размеров. А.Г. Ивахненко предложил метод последовательного иерархического формирования решающего правила на основе частных полиномов Колмогорова-Габора второго порядка. В задачах распознавания эффективность решающих правил зависит от различий законов распределения параметров  и
и  . Поэтому упростим частные полиномы, отбросив квадраты
. Поэтому упростим частные полиномы, отбросив квадраты  и
и  .
. . Составим два частных полинома
. Составим два частных полинома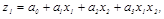 (2.3.32)
(2.3.32) (2.3.33)
(2.3.33) и
и  ,
,  уравнений для оценки коэффициентов
уравнений для оценки коэффициентов  и для оценки коэффициентов
и для оценки коэффициентов  :
: (2.3.34)
(2.3.34) (2.3.35)
(2.3.35)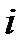 и второе по
и второе по 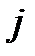 , сложим их и разделим на
, сложим их и разделим на  . Получим первое уравнение относительно неизвестных коэффициентов:
. Получим первое уравнение относительно неизвестных коэффициентов: (2.3.36)
(2.3.36) ,
, 
 .
.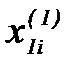 и
и  и определив средние значения, составим второе уравнение:
и определив средние значения, составим второе уравнение: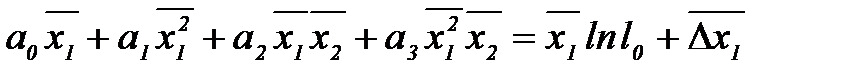 , (2.3.37)
, (2.3.37)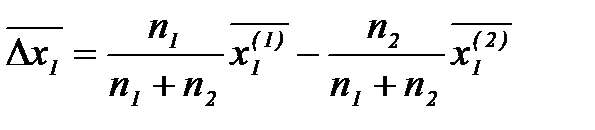
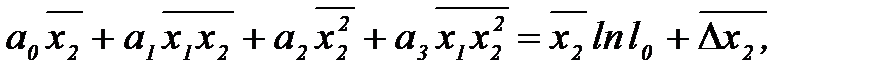 (2.3.38)
(2.3.38)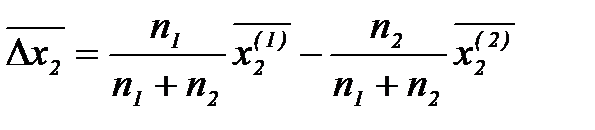
 и
и  и их усреднения:
и их усреднения: , (2.3.39)
, (2.3.39)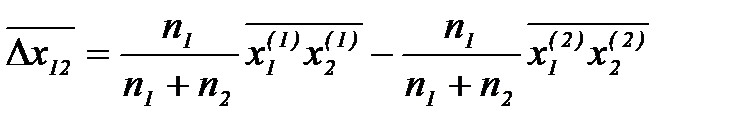 .
. . (2.3.40)
. (2.3.40) . (2.3.41)
. (2.3.41) и
и  получим таблицу промежуточных данных
получим таблицу промежуточных данных 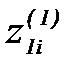 и
и  ,
,  и
и  .
.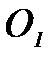







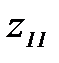
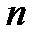

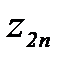


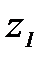 и
и 
 . (2.3.42)
. (2.3.42) ,
, 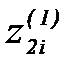 и
и 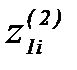 ,
,  . Будем иметь
. Будем иметь . (2.3.43)
. (2.3.43)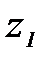 и
и  в (2.3.73)подставить выражения (2.3.70) и (2.3.71), то получим формулу для оценки логарифма отношения правдоподобия
в (2.3.73)подставить выражения (2.3.70) и (2.3.71), то получим формулу для оценки логарифма отношения правдоподобия (2.3.44)
(2.3.44) определяется через оценки коэффициентов
определяется через оценки коэффициентов  ,
,  ,
,  .
. имеет вид:
имеет вид: (2.3.45)
(2.3.45)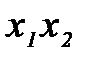 и
и  ,а не
,а не  и
и  или
или 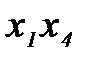 и
и  .Чтобы ответить на этот вопрос, необходимо сравнить различные решающие правила. Показателем их эффективности могут служить вероятности ошибок распознавания
.Чтобы ответить на этот вопрос, необходимо сравнить различные решающие правила. Показателем их эффективности могут служить вероятности ошибок распознавания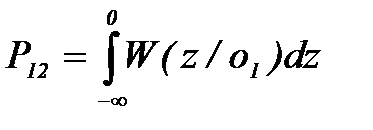 , (2.3.63)
, (2.3.63)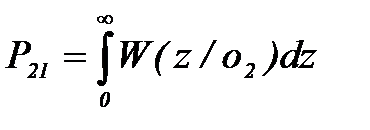 , (2.3.63)
, (2.3.63) (2.3.63)
(2.3.63) ,
, 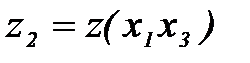 ,
,  ,
, 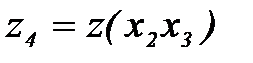 ,
,  ,
,  . Используя начальные исходные данные, составим первую промежуточную таблицу.
. Используя начальные исходные данные, составим первую промежуточную таблицу.







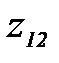
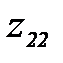




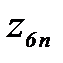
 соответствует вероятность распознавания
соответствует вероятность распознавания . (4.3.8)
. (4.3.8) .
.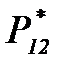 и
и  :
: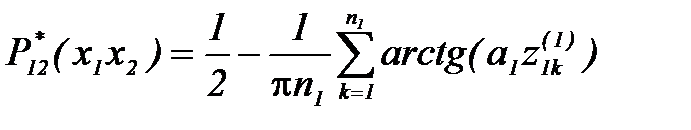 , (4.3.9)
, (4.3.9)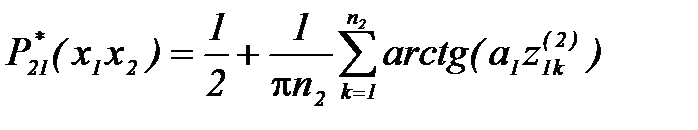 .
. . Результаты расчетов сведем в таблицу эффективностей пар - средних вероятностей распознавания для каждой пары
. Результаты расчетов сведем в таблицу эффективностей пар - средних вероятностей распознавания для каждой пары  , которые определим по формуле (4.3.8).
, которые определим по формуле (4.3.8).


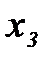

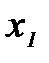

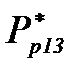



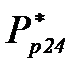


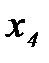
 и
и 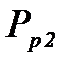 и вероятностью распознавания по двум параметрам
и вероятностью распознавания по двум параметрам  .
.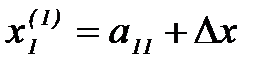 ,
,  ,
, ,
,  ,
, -нормальные ошибки измерений.
-нормальные ошибки измерений. ,
,  , то по методу минимума средней вероятности ошибки эффективность решающих правил равна:
, то по методу минимума средней вероятности ошибки эффективность решающих правил равна: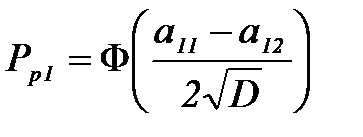 ,
,  , (4.3.10)
, (4.3.10) .
. примерно равно
примерно равно 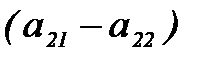 , то
, то 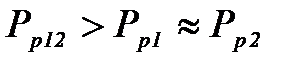 ;
;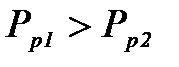 , то
, то 
 , т.е. если группируются эффективный и слабо эффективный параметры распознавания, то эффективность распознавания по двум параметрам мало будет отличаться от эффективности распознавания по одному (более эффективному).
, т.е. если группируются эффективный и слабо эффективный параметры распознавания, то эффективность распознавания по двум параметрам мало будет отличаться от эффективности распознавания по одному (более эффективному).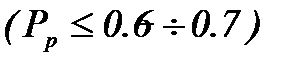 . Это связано с тем, что при небольших обучающих выборках использование мало эффективных параметров может ухудшить возможности распознавания. Покажем это на простом примере. Предположим, что параметры оценивались по экспериментальным данным, так что
. Это связано с тем, что при небольших обучающих выборках использование мало эффективных параметров может ухудшить возможности распознавания. Покажем это на простом примере. Предположим, что параметры оценивались по экспериментальным данным, так что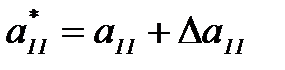 ,
,  ,
, ,
,  ,
, - ошибки оценивания.
- ошибки оценивания. будет равна
будет равна . (4.3.11)
. (4.3.11)
 могут принимать как положительные так и отрицательные значения, то возможны случаи, когда
могут принимать как положительные так и отрицательные значения, то возможны случаи, когда  . Это будет тогда, когда
. Это будет тогда, когда . (4.3.12)
. (4.3.12) , то вероятность этого неравенства можно вычислить. Выражение слева запишем в виде
, то вероятность этого неравенства можно вычислить. Выражение слева запишем в виде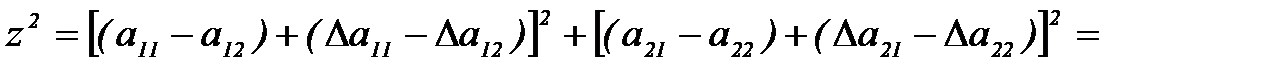
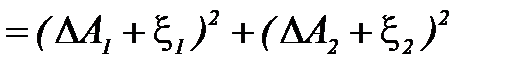 ,
, - нормальные случайные величины с нулевым средним и дисперсией
- нормальные случайные величины с нулевым средним и дисперсией  .
. -это закон Райса (обобщенный закон Релея)
-это закон Райса (обобщенный закон Релея) .
.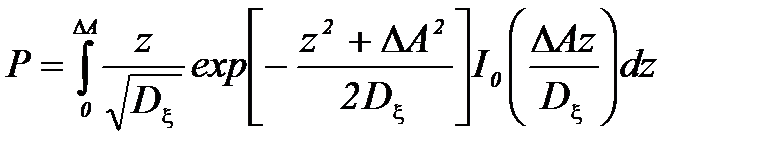 , (4.3.13)
, (4.3.13) .
. .
. получим формулу
получим формулу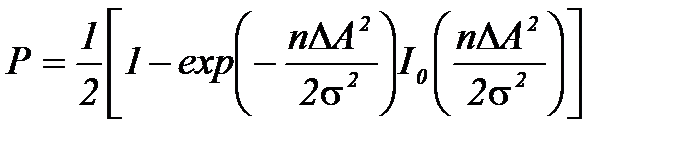 , (4.3.14)
, (4.3.14) - размер выборки, по которой оценивались неизвестные параметры.
- размер выборки, по которой оценивались неизвестные параметры. равна
равна .
. можно оценить по формуле
можно оценить по формуле . (4.3.15)
. (4.3.15)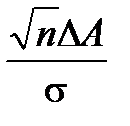 (аналог отношения сигнал / шум). Так как при этом увеличивается
(аналог отношения сигнал / шум). Так как при этом увеличивается  , то отрицательный эффект за счет ошибок формирования решающих правил проявляется слабо только при больших значениях сигнал / шум.
, то отрицательный эффект за счет ошибок формирования решающих правил проявляется слабо только при больших значениях сигнал / шум.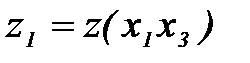 ,
,  и
и  , то на втором этапе отбора формируются три полинома
, то на втором этапе отбора формируются три полинома 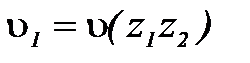 ,
,  и
и  , определяются их коэффициенты, оценивается эффективность и отбирается два лучших, на основе которых формируется отношение правдоподобия, например,
, определяются их коэффициенты, оценивается эффективность и отбирается два лучших, на основе которых формируется отношение правдоподобия, например, .
. и состоянии
и состоянии 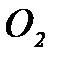 :1)
:1)  ; 2)
; 2) 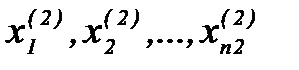 .Размеры выборок достаточны, чтобы построить гистограммы: 1)
.Размеры выборок достаточны, чтобы построить гистограммы: 1)  ; 2)
; 2) 
 . Если бы были известны законы распределения
. Если бы были известны законы распределения  и
и  , то можно было бы определить теоретические гистограммные вероятности
, то можно было бы определить теоретические гистограммные вероятности 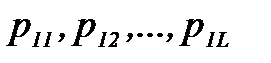 и
и 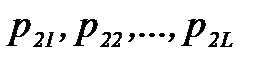 и для случайных величин
и для случайных величин 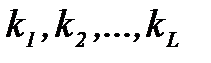 , где
, где 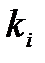 - число измерений выборки
- число измерений выборки  , попадающих в i-й интервал гистограммы, записать условные полиномиальные законы распределений
, попадающих в i-й интервал гистограммы, записать условные полиномиальные законы распределений (4.4.1)
(4.4.1) и
и  их оценками
их оценками  и
и 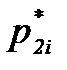 , составим отношение правдоподобия
, составим отношение правдоподобия (4.4.2)
(4.4.2) (4.4.3)
(4.4.3) определить гистограммные числа
определить гистограммные числа  , вычислить логарифмическую функцию отношение правдоподобия и сравнить её с порогом
, вычислить логарифмическую функцию отношение правдоподобия и сравнить её с порогом  . Эффективность алгоритма можно оценить, определив вероятности ошибок
. Эффективность алгоритма можно оценить, определив вероятности ошибок  и
и  , полагая порог
, полагая порог  . Логарифм отношения правдоподобия (4.4.3) как сумма биномиальных случайных величин имеет распределение, близкое к нормальному. Его математическое ожидание равно
. Логарифм отношения правдоподобия (4.4.3) как сумма биномиальных случайных величин имеет распределение, близкое к нормальному. Его математическое ожидание равно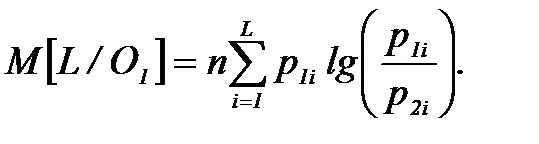
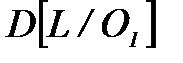 вычислим, учитывая, что случайные величины
вычислим, учитывая, что случайные величины  и
и  коррелированы и
коррелированы и 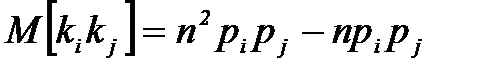 . В этом случае
. В этом случае 


