Обработка экспериментальных данных на основе моделей законов распределения вероятности с использованием сглаженных дельта-функций
При обработке выборок измерений нужно рассчитать основные статистические показатели, такие как выборочное среднее и дисперсию. Средне по выборке измерений находится так:
где, n – количество измерений в выборке, i - номер измерения в выборке (i = 1..n) Выборочная дисперсия находится так:
где, n – количество измерений в выборке, i - номер измерения в выборке (i = 1..n) Поскольку сканирование происходит на объекте с однородными характеристиками, то измерения в выборке могут быть связаны между собой. Показателем такой связи служит коэффициент корреляции.
где М - средние значения выборок измерений, i - номер измерения в выборке (i = 1..n) Далее, запишем формулы, связывающие размер выборки с оптимальным значением обобщенного параметра сглаживания для нормального закона распределения вероятностей:
где z- независимая переменная. С помощью этой зависимости можно с заданной длиной выборки оценить значение параметра сглаживания по формуле:
Таким образом, чтобы на практике выбрать параметр сглаживания, необходимо вычислить выборочный коэффициент асимметрии экспериментальных данных. Если
где Далее, запишем отношения правдоподобия:
l(xi)=
и решающее правило распознавания объекта
Согласно решающего правила
если
если
Показателями эффективности являются вероятности принять: а) нормальный объект за норму: P11= где (Р)і-решающие правило, i - номер измерения в выборке (i = 1..n); б) бракованный объект за брак: P12= где (Рb)і-решающие правило, i - номер измерения в выборке (i = 1..n); в)средняя вероятность распознавания: Pp=
В результате проведения серии экспериментов были получены графики зависимости оценок законов распределения вероятности на основе сглаженных дельта-функций.
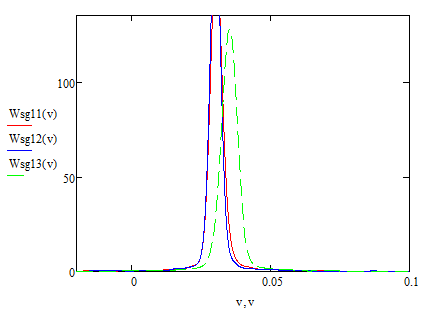
График 3.1.1 Оценки законов распределения вероятности на основе сглаженных дельта-функций, полученных для трех выборок нормы
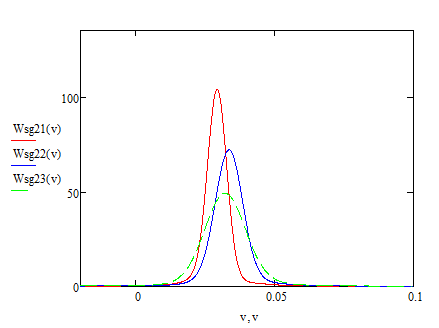
График 3.1.2. Оценки законов распределения вероятности на основе сглаженных дельта-функций, полученных для трех выборок брака
На графике 3.1.2 полученные оценки законов распределения сильно отличаються от оценок законов распределения, указанных на графике 3.1.1,что свидетельствует о наличие дефектних участков на пластине. По данным, полученных экспериментальным путем, проведена оценка законов распределение вероятности методом сглаженных дельта-функций, построены эмпирические решающие правила распознавания и найдена вероятность правильного распознавания. В результате чего, вероятность распознавания при обработки сигнала дает хороший результат, равный 0.7. Для улучшения качества обработки можно проводить расчет по стробам. Но следует отметить, что этот метод требует большего количества времени, то есть является более трудоемкими, а полученные результаты обработки увеличиваются лишь на десятые и равны 0.8.
|

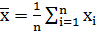 (3.1.1)
(3.1.1)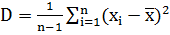 (3.1.2)
(3.1.2) (3.1.3)
(3.1.3)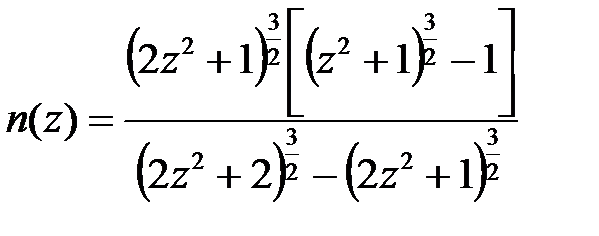 , (3.1.4)
, (3.1.4)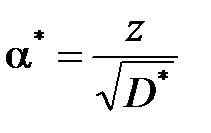 , (3.1.5) где
, (3.1.5) где 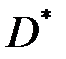 –выборочная дисперсия измерений.
–выборочная дисперсия измерений.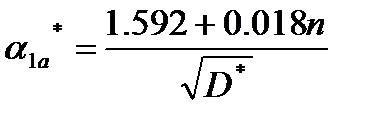 , (3.1.6)
, (3.1.6)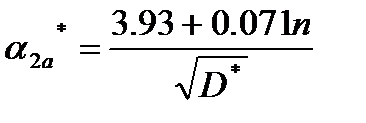 . (3.1.7)
. (3.1.7)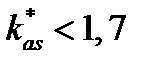 , то для вычисления параметра сглаживания используют формулу (3.1.6), а если
, то для вычисления параметра сглаживания используют формулу (3.1.6), а если 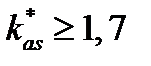 , то формулу (3.1.7).
, то формулу (3.1.7).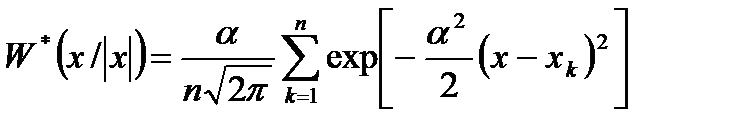 , (3.1.8)
, (3.1.8)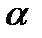 - параметр сглаживания,
- параметр сглаживания, 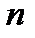 - длина выборки измерений,
- длина выборки измерений, 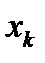 -
- 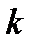 -ое измерения экспериментальных данных
-ое измерения экспериментальных данных 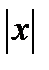 .
.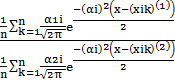 (3.1.9)
(3.1.9) . (3.1.10)
. (3.1.10) (3.1.11)
(3.1.11)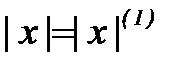 , т.е. измерения принадлежат объектам класса
, т.е. измерения принадлежат объектам класса 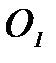 , и наоборот
, и наоборот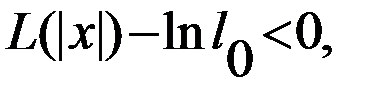 (3.1.12)
(3.1.12)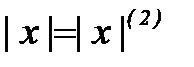 .
.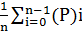 , (3.1.13)
, (3.1.13)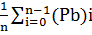 , (3.1.14)
, (3.1.14)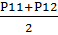 (3.1.15)
(3.1.15)