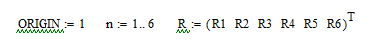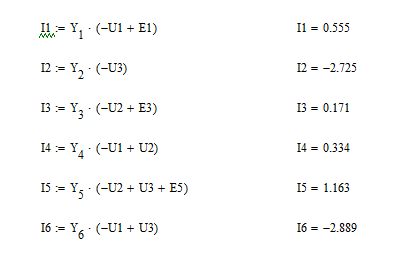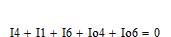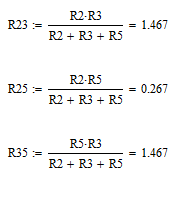Решение задачи 1.1

Поставщик	S1	S2	S3	S4	S5
Кол-во	25K	35K	30K	45K	15K

 

Требуется:

1. Сбалансировать задачу.

2. Минимизировать суммарные транспортные издержки (найти наилучший план перевозок). Представить матрицу перевозок и найти величину затрат. Имеется ли альтернативный план перевозок?

3. Если имеется задача с дефицитом, указать какие заказчики получат товар в недостаточном количестве (указать величину дефицита); если имеется задача с избытком, то указать какие из поставщиков не смогут реализовать полностью свой товар (указать величину излишков).

4. Найти наихудший план перевозок и разность между наилучшим и наихудшим планами перевозок.

5. Найти наилучший план перевозок в случае, если некоторые из каналов окажутся закрытыми (см. таблицу ниже). Насколько возрастут издержки?

 

№ варианта (последняя цифра)	Закрытые каналы
	От S2 к D7	От S3 к D6	От S5 к D4
	От S3 к D5	От S4 к D1	От S5 к D7
	От S1 к D2	От S2 к D9	От S3 к D4
	От S1 к D10	От S3 к D7	От S4 к D8
	От S2 к D9	От S4 к D8	От S5 к D4
	От S2 к D7	От S3 к D4	От S4 к D1
	От S1 к D10	От S2 к D7	От S5 к D4
	От S1 к D2	От S3 к D6	От S4 к D3
	От S1 к D7	От S3 к D5	От S4 к D8
	От S1 к D9	От S3 к D5	От S4 к D3

 

 

Содержание

1. Задача 1.1………………………………………………………………….….3

1.1. Решение задачи 1.1 в MathCad………………………………………….4

2. Задача 1.2……………………………………………………………………...8

2.1. Решение задачи 1.2 ………………………………………………………9

3. Задача 2.1……………………………………………………………………..14

3.1. Решение задачи 2.1 ……………………………………………………..15

4. Задача 2.2……………………………………………………………………...24

4.1. Решение задачи 2.2 ………………………………………………………25

 

Задача 1.1

Для цепи постоянного тока, заданной в виде графа, составить электрическую схему, включив в схему все заданные вариантом элементы; обозначить положительное направление токов. Для полученной цепи необходимо:

1. По заданному графу составить подробную электрическую схему анализируемой цепи, на схеме произвольно указать положительные направления токов в ветвях и обозначить их, пронумеровать узлы, и последний (четвертый) принять в качестве «базового».

2. Определить токи всех ветвей, используя метод узловых напряжений.

3. Определить ток первой ветви I₁, используя метод эквивалентного генератора.

 

Решение задачи 1.1

1.

Рис.1

Исходные данные:

Сопротивления, Ом:

Источники ЭДС, В:

Источники тока, А:

2. Метод узловых напряжений

Определим матрицу проводимостей ветвей:

Определим собственные и взаимные проводимости узлов. Узел 1 соединяет ветви 1,4,6, узел 2—ветви 3,4,5, узел 3—ветви 2,5,6.

Матрица собственных и взаимных проводимостей

Определим узловые токи с учётом выбранных направлений источников ЭДС и тока

Положительным считаем ток, направленный к узлу, отрицательным—направленный от узла. Источники ЭДС преобразуем в эквивалентные источники тока.

 

Решение системы уравнений узловых потенциалов представляем в матричной форме

 

Определяем токи в ветвях:

Отрицательные значения токов свидетельствуют о противоположном направлении протекания токов по сравнению с заданными по схеме.

 

Проверяем баланс токов в узлах цепи по первому закону Кирхгофа:

 

Первый узел:

Второй узел:

Третий узел:

 

Расчет токов выполнен правильно, так как сумма токов в каждом независимом узле равна нулю.

 

3. Нахождение I₁ методом эквивалентного генератора:

 

Составляем схему замещения электрической цепи для нахождения Rэ

 

 

Преобразуем треугольник сопротивлений в звезду

 

Находим эквивалентное сопротивление

Вычисляем напряжение холостого хода

Находим ток I₁