Определение криволинейного интеграла первого рода.
1. Федеральный закон Российской Федерации «О пожарной безопасности» от 18 ноября 1994 года. 2. Боевой Устав пожарной охраны (Приложение 2) приказа МВД от 05.07.1995 № 257. 3. Устав службы пожарной охраны (Приложение 1) приказа МВД от 05.07.1995 № 257. 4. Правила охраны труда в подразделениях Государственной противопожарной службы МЧС России от 31.12.2002 г №630. 5. Повзик Я.С. Пожарная тактика: М., ЗАО спецтехника, 2001г. 6. Повзик Я.С. Справочник руководителя тушения пожара М ЗАО спецтехника, 2001г. 7. ГОСТ 12.1.114-82* Техника пожарная, обозначения условные графические.
Геометрическое и физическое применение криволинейного интеграла Криволинейный интеграл первого рода Определение криволинейного интеграла первого рода. Рассмотрим в трехмерном пространстве с заданной декартовой системой координат ОXYZ некоторую кривую Г (см. рис. 1). Декартовы координаты точек кривой будем обозначать через (х, у, z).
Определение 1. Кривая, заданная уравнением
называется непрерывной кусочно-гладкой, если функции
Рис.1. К определению кривой. Пусть на кривой Г
Рис. 2. Разбиение кривой Г.
Зададим разбиение T кривой Г точками A = N o, N 1, N 2, …, Nn = B, (см. рис. 2). На каждой из дуг ∪ Nk Nk +1 выберем по произвольной точке Mk с координатами (ξ k, η k, ζ k) и составим интегральную сумму:
где Δ sk – длина дуги ∪ Nk Nk +1.
Определение 2. Криволинейным интегралом первого рода от функции
Для криволинейного интеграла по замкнутой кривой Г используется иное обозначение:
Существование криволинейного интеграла устанавливает следующая теорема:
Теорема 1. Если Г – непрерывная кусочно-гладкая кривая и функция f (M) непрерывна на ней, то криволинейный интеграл первого рода (3) от функции f (M) существует и определен однозначно.
Теорема 2. Если кривая Г задана уравнениями (1), а функция f (M) непрерывна на этой кривой, то криволинейный интеграл первого рода от функции f (M) находится по формуле
Замечание. При использовании формулы (4) следует обращать внимание на то, чтобы при изменении параметра t от а до b дифференциалы ds и dt были неотрицательными, поскольку выражение
задает элемент длины дуги, который отрицательным быть не может.
ПРИМЕР 1. Найти интеграл
Рис.3. К примеру 1. Рис.4. К примеру 2.
ПРИМЕР 2. На кривой Г, заданной параметрически уравнениями точками С уменьшением длин дуг ∪ Nk Nk +1 разбиения исходной кривой интегральная сумма приближается к искомой массе. В пределе получаем:
Замечание. В случае кривой на плоскости:
сохраняются определения и остаются справедливыми все теоремы, сформулированные выше. В соответствующих формулах нужно лишь убрать третью координату z (t) или ζ k. ПРИМЕР 3. Вычислить интеграл
Рис.5. К примеру 3.
Пусть для определенности a > b. Введем параметризацию дуги:
|

 Sп.м² Q, л/с
Sп.м² Q, л/с

 204
204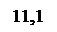






















 Литература.
Литература. ,
, 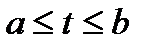 , (1)
, (1) и
и  непрерывны на отрезке
непрерывны на отрезке  и
и  отрезок может быть разбит точками
отрезок может быть разбит точками  на конечное число отрезков таким образом, что на каждом из этих частичных отрезков функции
на конечное число отрезков таким образом, что на каждом из этих частичных отрезков функции  и
и  имеют непрерывные производные, не обращающиеся одновременно в
имеют непрерывные производные, не обращающиеся одновременно в  .
.
 , где
, где 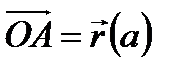 ,
,  задана непрерывная функция
задана непрерывная функция  , где
, где  – точка на кривой.
– точка на кривой.

 , (2)
, (2) по кривой Г называется предел интегральной суммы (2) при бесконечном увеличении числа n точек деления Nk и бесконечном уменьшении длин дуг ∪ Nk Nk +1, если этот предел существует и не зависит ни от способа разбиения T, ни от выбора точек Mk на дугах:
по кривой Г называется предел интегральной суммы (2) при бесконечном увеличении числа n точек деления Nk и бесконечном уменьшении длин дуг ∪ Nk Nk +1, если этот предел существует и не зависит ни от способа разбиения T, ни от выбора точек Mk на дугах: (3)
(3)
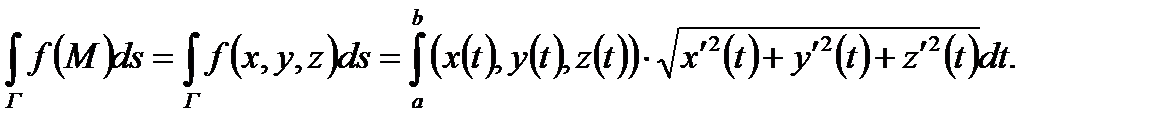 (4)
(4)
 , где кривая Г – дуга окружности с центром в начале координат и радиуса 1 между точками А (0, 1) и В (1, 0) (см. рис. 3). Введем на кривой Г параметризацию:
, где кривая Г – дуга окружности с центром в начале координат и радиуса 1 между точками А (0, 1) и В (1, 0) (см. рис. 3). Введем на кривой Г параметризацию:  . Тогда
. Тогда  . Здесь модуль раскрывается со знаком «–» поскольку при интегрировании от точки А до точки В параметр t изменяется в интервале от π /2 до 0 и, следовательно, dt < 0. Применяя формулу (4), получим:
. Здесь модуль раскрывается со знаком «–» поскольку при интегрировании от точки А до точки В параметр t изменяется в интервале от π /2 до 0 и, следовательно, dt < 0. Применяя формулу (4), получим:


 , распределена масса с плотностью
, распределена масса с плотностью  . Определить массу кривой. Кривая Г представляет собой два витка спирали (см. рис.4). Для определения ее массы воспользуемся процедурой, аналогичной применявшейся при введении понятия криволинейного интеграла. Проведем разбиение T кривой Г
. Определить массу кривой. Кривая Г представляет собой два витка спирали (см. рис.4). Для определения ее массы воспользуемся процедурой, аналогичной применявшейся при введении понятия криволинейного интеграла. Проведем разбиение T кривой Г на элементарные дуги ∪ Nk Nk +1. На каждой дуге выберем по точке Mk и будем считать, что плотность кривой на этой дуге постоянна и равна значению ρ(Mk) плотности в точке Mk. Тогда масса элементарной дуги равна произведению плотности на длину дуги: Δ mk = ρ(Mk)·Δ sk. Масса всей кривой равна сумме масс всех элементарных дуг:
на элементарные дуги ∪ Nk Nk +1. На каждой дуге выберем по точке Mk и будем считать, что плотность кривой на этой дуге постоянна и равна значению ρ(Mk) плотности в точке Mk. Тогда масса элементарной дуги равна произведению плотности на длину дуги: Δ mk = ρ(Mk)·Δ sk. Масса всей кривой равна сумме масс всех элементарных дуг:  . Полученное выражение представляет собой интегральную сумму криволинейного интеграла первого рода
. Полученное выражение представляет собой интегральную сумму криволинейного интеграла первого рода  функции ρ(М) по дуге Г.
функции ρ(М) по дуге Г.
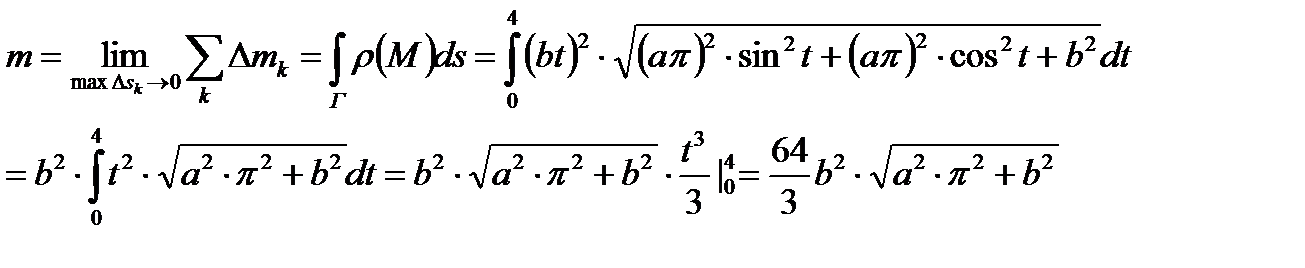
 (5)
(5) , где Г – четверть эллипса
, где Г – четверть эллипса  , лежащая в первом квадрате (см. рис. 5).
, лежащая в первом квадрате (см. рис. 5).
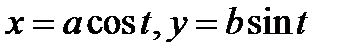 ,
, . Тогда, используя теорему 2, получаем
. Тогда, используя теорему 2, получаем



