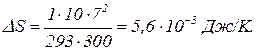Изменения энтропии при теплообмене

Задача 1. В идеальном калориметре находится вода массы М при температуре T01=300°К. В воду бросили брусок массы m=10 г<<M с удельной теплоемкостью 1 Дж/г×К при температуре Т02=293°К. Вода стала отдавать, а брусок получать тепло, так что система стала приближаться к равновесному состоянию.
а) Пусть за малое время температура бруска увеличилась на малую величину DТ2. На сколько изменится энтропия воды? бруска? всей системы?
б) Чему равно полное изменение энтропии всей системы к моменту установления теплового равновесия.

Решение. Так как масса воды гораздо больше массы бруска, можно считать, что при теплообмене температура воды не изменилась.

а) Брусок получает количество теплоты, равное
. (1)
При этом его энтропия увеличивается на
(2)
Вода отдает тепло DQ2, поэтому при теплопередаче ее энтропия уменьшается на
. (3)
Изменение энтропии всей системы при этом
(4)
Поскольку T1>T2, постольку первое слагаемое в выражении (4) больше, чем второе. Энтропия увеличивается.

б) Полное изменение энтропии всей системы равно сумме малых изменений при передаче малых количеств тепла:
(5)
У каждого слагаемого в первой сумме правой части уравнения (5) свой знаменатель. При вычислении первой суммы воспользуемся уже известным для нее результатом
(6)
Тогда
(7)

Во второй сумме уравнения (5) все слагаемые имеют один и тот же знаменатель, поэтому
(8)
В итоге находим:
(9)
Учтем, что T01-T02«T01, T02. Под знаком логарифма стоит величина, близкая к единице. Можно записать:
(10)

Так как график ln x в малой области изменения х выглядит приближенно как линейный, легко вычислить : он равен отклонению от единицы, умноженному на тангенс угла наклона графика ln x к оси ОX в точке х=1. Этот тангенс равен 1. Поэтому . Данный результат можно было получить сразу без хлопот из (5) или (7), если учесть, что T2 почти не изменяется. Таким образом,
(11)
Подставляя данные задачи, получаем следующее значение увеличения энтропии:

Из общего решения задачи, задаваемого уравнением (11), следует, что при большей начальной разнице температур бруска и воды, то есть при большей удаленности начального состояния системы от равновесного состояния, процесс теплопередачи сопровождается большим увеличением энтропии.

ВЫВОД: Разность энтропий равновесного и начального состояний является мерой удаленности начального состояния от равновесного.

Теплообмен происходит необратимо. Это означает, если нагревание бруска от воды идет самопроизвольно, то отдача тепла от бруска к воде не может происходить самопроизвольно. Процессы, происходящие естественным путем (самопроизвольно), сопровождаются увеличением энтропии.

Вопрос 1. Можно ли каким-нибудь способом вернуть описанную в задаче систему в исходное состояние? Что можно будет сказать об энтропии всего мира в результате описанного выше процесса?

Если энтропия какого-либо тела уменьшается, то это происходит только за счет того, что энтропия каких-либо других тел увеличивается, причем на величину не меньшую, чем наблюдаемое уменьшение.

Используя понятие энтропии, второе начало термодинамики можно сформулировать следующим образом: при всех процессах, протекающих в природе самопроизвольно, энтропия всего мира увеличивается или остается неизменной.

Вопрос 2. Можно ли систему из двух тел, находящихся при разных температурах T1 и T2, T1¹T2, перевести в равновесное состояние (T*1=T*2) без увеличения энтропии?

Задание. Используя формулировку второго начала термодинамики в терминах энтропии, покажите необходимость существования холодильника у тепловой машины.

Замечание. Тепловая машина преобразует неупорядоченный вид энергии (тепловая энергия хаотического движения молекул) в упорядоченный вид (кинетическая энергия маховика или потенциальная энергия поднятого груза, сжатой пружины.) Это преобразование происходит ценой увеличения энтропии холодильника. Увеличение энтропии является платой за производство работы.