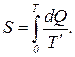Аналогично внутренней энергии энтропия также является функцией состояния. Чтобы убедиться в этом, рассмотрим идеальный газ. Пусть он переходит из состояния ( A ) в состояние ( B ). Можно придумать бесчисленное число способов перехода. Пусть каждый из способов перехода на PV - диаграмме описывается своей зависимостью P=P(V). Рассмотрим бесконечно малый процесс, сопровождающийся бесконечно малым расширением dV. В таком процессе газ получает бесконечно малое тепло
Аналогично внутренней энергии энтропия также является функцией состояния. Чтобы убедиться в этом, рассмотрим идеальный газ. Пусть он переходит из состояния ( A ) в состояние ( B ). Можно придумать бесчисленное число способов перехода. Пусть каждый из способов перехода на PV - диаграмме описывается своей зависимостью P=P(V). Рассмотрим бесконечно малый процесс, сопровождающийся бесконечно малым расширением dV. В таком процессе газ получает бесконечно малое тепло
dQ=dU+P(V)dV. (1)
Учтем, что dU=CVdT, тогда бесконечно малое изменение энтропии в этом бесконечно малом процессе будет равно
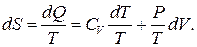 (2)
(2)
Из уравнения состояния следует, что
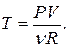 (3)
(3)
После подстановки (3) во второе слагаемое выражение (2) преобразуется так:
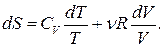 (4)
(4)
Полное изменение энтропии при переходе из состояния ( A ) в состояние ( B ) равно сумме всех бесконечно малых изменений (4)
 (5)
(5)
Выражение (5) показывает, что изменение энтропии n молей идеального газа при любой зависимости P(V) или любом пути перехода из (A)в (B) одно и то же. Это означает, что энтропия газа в любом состоянии зависит только от параметров этого состояния, но не зависит от способа попадания в него. [Причина данного свойства энтропии станет более ясной при рассмотрении микроскопической картины изменения состояний].
Из проведенного выше анализа следует вывод: если тело участвует в каком-либо циклическом процессе, то при возвращении тела в исходное состояние, энтропия тела принимает первоначальное значение.
Полученный вывод для идеального газа справедлив для любой физической системы. Энтропия любой термодинамической системы является функцией состояния. Любое тело можно проградуировать по энтропии аналогично тому, как возможна градуировка по внутренней энергии. Можно вообразить следующую идеализированную ситуацию. Надо взять тело при температуре, близкой к абсолютному нулю. Затем сообщать бесконечно малые порции тепла и каждый раз отмечать температуру и другие параметры состояния. При этом энтропия увеличивается на 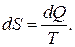 По мере подведения тепла энтропия будет увеличиваться, так что для любого состояния будет в конце концов определена энтропия
По мере подведения тепла энтропия будет увеличиваться, так что для любого состояния будет в конце концов определена энтропия
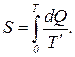
Если над телом совершается только работа, а тепло не подводится и не отводится, то энтропия тела не изменяется. Из этого следует, что адиабатический процесс над газом происходит при постоянстве энтропии - адиабата является изоэнтропой.

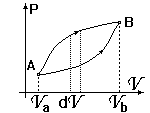
 Аналогично внутренней энергии энтропия также является функцией состояния. Чтобы убедиться в этом, рассмотрим идеальный газ. Пусть он переходит из состояния ( A ) в состояние ( B ). Можно придумать бесчисленное число способов перехода. Пусть каждый из способов перехода на PV - диаграмме описывается своей зависимостью P=P(V). Рассмотрим бесконечно малый процесс, сопровождающийся бесконечно малым расширением dV. В таком процессе газ получает бесконечно малое тепло
Аналогично внутренней энергии энтропия также является функцией состояния. Чтобы убедиться в этом, рассмотрим идеальный газ. Пусть он переходит из состояния ( A ) в состояние ( B ). Можно придумать бесчисленное число способов перехода. Пусть каждый из способов перехода на PV - диаграмме описывается своей зависимостью P=P(V). Рассмотрим бесконечно малый процесс, сопровождающийся бесконечно малым расширением dV. В таком процессе газ получает бесконечно малое тепло 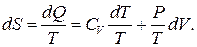 (2)
(2) 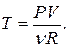 (3)
(3) 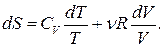 (4)
(4) (5)
(5) 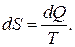 По мере подведения тепла энтропия будет увеличиваться, так что для любого состояния будет в конце концов определена энтропия
По мере подведения тепла энтропия будет увеличиваться, так что для любого состояния будет в конце концов определена энтропия