Обратимый тепловой двигатель. Задача 2.а) Какое количество тепловой энергии безвозвратно теряется при использовании регенератора с указанным в лекции делением на секции
Задача 2. а) Какое количество тепловой энергии безвозвратно теряется при использовании регенератора с указанным в лекции делением на секции. Задача 3. Предположим, описанный выше тепловой двигатель с идеальным регенератором совершает работу по подъему некоторого груза в поле тяжести. После подъема груза ему позволили опускаться, совершая работу над тепловым двигателем. При этом состояние газа в цилиндре изменяется по тому же циклу, но в противоположном направлении. Опишите энергетические превращения в этом процессе. Можно предложить сравнительно быстрый вывод формулы КПД обратимой тепловой машины, в котором не проводится непосредственный расчет теплоты, полученной от нагревателя, и совершенной машиной работы. Решение. Пусть газ в цилиндре (рабочее тело) изменяет состояние по описанному выше циклу и пусть также используется идеальный регенератор. Разобьем область значений объема газа на малые части величиной DV. Вертикальная полоска на PV - диаграмме вырезает на изотермах отрезки. На отрезке высокотемпературной изотермы газ получает тепло DQ1 от нагревателя. Оно равно совершаемой газом работе на данном участке
На отрезке низкотемпературной изотермы газ отдает тепло DQ2 холодильнику. Оно равно работе, совершаемой над газом на данном участке
При заданном объеме справедлив закон:
поэтому Поскольку соотношение (4) справедливо для любого участка значений объема газа, справедливо следующее:
Теперь учтем, что КПД обратимой тепловой машины -
повышается, при увеличении T1 и уменьшении T2.
|

 (1)
(1) . (2)
. (2) (3)
(3)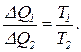 (4)
(4) (5)
(5) - (6)
- (6)


