Обратимый тепловой двигатель
Использование описанного выше регенератора не вполне избавят от безвозвратной передачи тепла холодильнику. Переход от последней ступени регенератора при температуре 310°К к холодильнику сопровождается передачей холодильнику количества теплоты, равного 10×СV. Так что последний шаг нагревания в изохорическом процессе 4®1 придется сделать не с помощью регенератора, а с помощью нагревателя. Можно добиться сокращения непроизводительных потерь тепла, увеличив число ступеней регенератора. При бесконечно частом разбиении потери стремятся к нулю. Регенератор становится идеальным. Замечательно, что при этом тепло Q41=CV(T1-T2) уже не отдается холодильнику, а вовлекается в производительный оборот - возвращается рабочему телу, - поэтому полное полученное от нагревателя тепло будет теперь равно Если вместо того, чтобы получать, будем совершать над двигателем работу, так что цикл будет происходить в обратном направлении, то на участке 4®3 тепло от холодильника будет приниматься рабочим телом. На участке 2®1 рабочее тело будет отдавать тепло нагревателю. В итоге тепло от более холодного тела будет передаваться более горячему. Двигатель, работающий по обратному циклу - уже не двигатель, а холодильник, или тепловой насос. Тепловой двигатель, работающий по описанному выше циклу с идеальным регенератором, называется обратимой тепловой машиной. Чтобы лучше понять смысл этого названия рассмотрим следующую физическую ситуацию. Предположим, описанный выше тепловой двигатель с идеальным регенератором совершает работу по подъему некоторого груза в поле тяжести. После подъема груза ему позволили опускаться, совершая работу над тепловым двигателем. Во-первых, процессы, происходившие в тепловом двигателе на первом этапе, при опускании груза будут те же самые, но происходить будут в противоположном порядке. После завершения второго этапа не только тепловая машина вернется в исходное состояние, но и к нагревателю возвратится отданное тепло Q1, и холодильник возвратит ранее полученное тепло Q2. Термодинамическое состояние тепловой машины и всего окружающего мира станут такими, как до начала работы машины. Можно предложить довольно общий вывод формулы КПД обратимой тепловой машины, в котором не проводится непосредственный расчет полученной от нагревателя теплоты и совершенной машиной работы. Пусть газ в цилиндре (рабочее тело) изменяет состояние по описанному выше циклу и пусть также используется идеальный регенератор. Разобьем область значений объема газа на малые отрезки величиной DV. Вертикальная полоска на PV - диаграмме вырезает на изотермах отрезки. На отрезке высокотемпературной изотермы газ получает тепло DQ1 от нагревателя. Оно равно совершаемой газом работе на данном участке: DQ1=P1DV. (5) На отрезке низкотемпературной изотермы газ отдает тепло DQ2 холодильнику. Оно равно работе, совершаемой над газом на другом участке: DQ2=P2DV.. (6) При заданном объеме справедлив закон
поэтому Так как соотношение (8) справедливо для любого участка значений объема газа, то справедливо следующее:
Коэффициент полезного действия обратимой тепловой машины можно повышать, увеличивая температуру нагревателя или уменьшая температуру холодильника. По этой причине не тепловых электростанциях стремятся использовать пар для турбин при максимально высокой температуре. Действие обратимой тепловой машины не связано с каким-либо конкретным циклом. Главный признак обратимости состоит в том, чтобы при обращении хода машины можно было возвратить состояние и машины и всего окружающего мира. Формула (10) является общей для всех обратимых тепловых машин.
|


 Вернемся к циклу, рассмотренному на предыдущей лекции. Он состоит из двух изотерм при температурах T1 и T2 и двух изохор при объемах V 1 и V 2 (T1>T2 и V1<V2). Было найдено, что КПД данного цикла равен
Вернемся к циклу, рассмотренному на предыдущей лекции. Он состоит из двух изотерм при температурах T1 и T2 и двух изохор при объемах V 1 и V 2 (T1>T2 и V1<V2). Было найдено, что КПД данного цикла равен  . (2)
. (2)  отбирать у нагревателя для пополнения внутренней энергии газа. Если бы удалось сохранить сбрасываемое тепло на этапе 2-3, то доля внутренней энергии нагревателя, превращенная в работу, увеличилась бы. Устройство сохранения и дальнейшего использования тепла представляет собой регенератор. Таким регенератором мог бы служить специальный термостат, разделенный на множество секций адиабатическими перегородками. Каждая секция имеет свою температуру (приблизительно соответствующую своему участку изохор 2-3 и 4-1), так что последовательность всех секций в целом обеспечивает более или менее плавный переход от T1 к T2. В частности, при T1=400°К и T2=300°К секции могут иметь, например, температуры 390°К, 380°К,... 320°К, 310°К. Перемещая тепловой контакт рабочего цилиндра от секций с высокой температурой к секциям с низкой температурой мы будем запасать энергию, отдаваемую газом, в регенераторе. После изотермического сжатия 3-4 тепловой контакт перемещаем снизу вверх, от секций с низкой температурой к секциям с высокой температурой. При этом используется ранее запасенная в регенераторе тепловая энергия.
отбирать у нагревателя для пополнения внутренней энергии газа. Если бы удалось сохранить сбрасываемое тепло на этапе 2-3, то доля внутренней энергии нагревателя, превращенная в работу, увеличилась бы. Устройство сохранения и дальнейшего использования тепла представляет собой регенератор. Таким регенератором мог бы служить специальный термостат, разделенный на множество секций адиабатическими перегородками. Каждая секция имеет свою температуру (приблизительно соответствующую своему участку изохор 2-3 и 4-1), так что последовательность всех секций в целом обеспечивает более или менее плавный переход от T1 к T2. В частности, при T1=400°К и T2=300°К секции могут иметь, например, температуры 390°К, 380°К,... 320°К, 310°К. Перемещая тепловой контакт рабочего цилиндра от секций с высокой температурой к секциям с низкой температурой мы будем запасать энергию, отдаваемую газом, в регенераторе. После изотермического сжатия 3-4 тепловой контакт перемещаем снизу вверх, от секций с низкой температурой к секциям с высокой температурой. При этом используется ранее запасенная в регенераторе тепловая энергия. (3)
(3)  (4)
(4) (7)
(7) (8)
(8)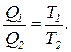 (9)
(9) 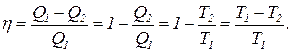 (10)
(10)


