Фононы. Статистические свойства фононного газа
Если кристаллическое тело рассматривать как систему N связанных частиц, то смещение одного из атомов из положения равновесия влечет за собой смещение других соседних с ним атомов. В результате этого в кристалле возникает упругая волна. Дойдя до границы кристалла, волна отражается. При наложении прямой и отраженной волн образуется стоячая волна. В соответствии с гипотезой Де Бройля с каждой бегущей монохроматической волной связаны энергия и импульс, определяемые соотношениями
введенными по аналогии с теорией фотонов. Волна, несущая энергию и импульс, определяемые формулами (4.2), в каком-то отношении ведет себя как частица. Частица, уподобляемая звуковой волне в вышеуказанном смысле, называется фононом. Фонон во многих отношениях ведет себя так, как если бы он был частицей с энергией и импульсом (4.2). Однако в отличие от обычных частиц (электронов, протонов, фотонов) фонон не может возникнуть в вакууме – для своего возникновения и существования фонон нуждается в некоторой среде. Подобного рода частицы называются квазичастицами. Фононы хорошо приспособлены для описания слабых коллективных возбуждений атомов в кристалле. Между последовательными столкновениями фонон движется свободно, и если «длина свободного пробега» его достаточно велика по сравнению с постоянной кристаллической решетки, то возбужденное состояние кристалла можно в известном отношении рассматривать как фононный газ, подобно тому, как электромагнитное излучение можно представить как фотонный газ, заполняющий полость. Формально оба представления весьма схожи – и фотоны, и фононы подчиняются одной и той же статистике Бозе-Эйнштейна. Однако между фотонами и фононами имеется существенное различие: в то время как фотоны являются истинными частицами, фононы являются квазичастицами. Так как волны, длина которых меньше удвоенного межатомного расстояния, не имеют физического смысла, то существует минимальная длина волны упругих волн в кристалле:
где d – расстояние между соседними атомами в кристаллической решетке. Минимальной длине волны соответствует максимальная частота колебаний:
где Согласно этому энергетические уровни фононов в кристалле ограничены сверху уровнем с максимальной энергией фононов (рис. 4.2)
Для вычисления энергии фононного газа в кристалле воспользуемся статистическим методом. Для этого на схеме энергетических уровней фононов выделим узкую полосу с энергиями в интервале от ε до ε + dε, где dε – ширина полосы энергетических уровней.
где dn – число фононов в полосе dε. Это число фононов dn определяется функцией распределения фононов по энергиям f (ε) и числом состояний dZ в полосе dε:
Поскольку фононы подчиняются статистике Бозе-Эйнштейна, то:
Число состояний dZ в полосе dε нам предстоит вычислить. Для этого рассмотрим фазовое пространство, характеризуемое шестью координатами (x, y, z, px, py, pz). Чтобы подсчитать число квантовых состояний в элементе объема данного фазового пространства, надо этот элемент объема разделить на объем элементарной ячейки равный
где V – объем кристалла. Учитывая связь между импульсом и энергией фонона
Формула (8) не учитывает возможных видов поляризации волны. В твердой среде вдоль некоторого направления могут распространяться три разные волны с одним и тем же значением частоты ω, отличающиеся направлением поляризации: одна продольная и две поперечные со взаимно перпендикулярными направлениями колебаний. В соответствии с этим формулу (4/8) нужно видоизменить следующим образом:
где Положим для простоты
Максимальную энергию фононов εmax в кристалле можно найти, приравнивая полное число всех квантовых состояний числу степеней свободы, равному 3N
Отсюда
Исключив из равенств (4.9) и (4.10) скорость
Тогда энергия фононов в полосе значений энергий dε равна
|

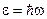 ,
, 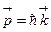 , (4.2)
, (4.2) ,
, ,
, – скорость упругих волн в кристалле.
– скорость упругих волн в кристалле.
 . (4.3)
. (4.3) Тогда энергия фононов в полосе dε равна:
Тогда энергия фононов в полосе dε равна: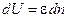 , (4.4)
, (4.4) , (4.5)
, (4.5)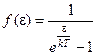 , (4.6)
, (4.6) . Тогда, если мы хотим подсчитать число состояний dZ в интервале импульсов от р до р+dp, надо объем, заключенный между двумя сферами с радиусами р и р+dp, умножить на V и разделить на
. Тогда, если мы хотим подсчитать число состояний dZ в интервале импульсов от р до р+dp, надо объем, заключенный между двумя сферами с радиусами р и р+dp, умножить на V и разделить на 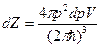 , (4.7)
, (4.7) , получим:
, получим: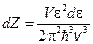 . (4/8)
. (4/8)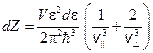 ,
,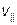 – фазовая скорость продольных, а
– фазовая скорость продольных, а 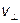 – поперечных упругих волн.
– поперечных упругих волн.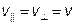 , тогда
, тогда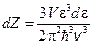 . (4.9)
. (4.9)
 , (4.10)
, (4.10)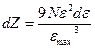 . (4.11)
. (4.11)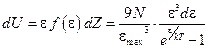 . (4.12)
. (4.12)


