В этом случае имеет место распределение Бозе-Эйнштейна:
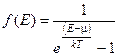 , (3.8)
, (3.8)
где 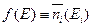 - среднее число частиц, находящихся в состоянии с номером
- среднее число частиц, находящихся в состоянии с номером 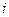 ,
,  – энергия частиц в этом состоянии.
– энергия частиц в этом состоянии.
 Значения химического потенциала
Значения химического потенциала  в распределении (3.8) не могут быть положительными, т.е.
в распределении (3.8) не могут быть положительными, т.е.  , ибо в противном случае при
, ибо в противном случае при  среднее число
среднее число 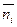 оказалось бы отрицательным.
оказалось бы отрицательным.
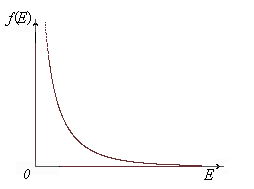
 График функции распределения Бозе-Эйнштейна в случае
График функции распределения Бозе-Эйнштейна в случае 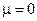 для температуры
для температуры  представлен на рис. 3.5.
представлен на рис. 3.5.
Как видно из рисунка, с уменьшением энергии функция распределения Бозе-Эйнштейна стремиться к бесконечности, т.е. среднее число бозонов в квантовом состоянии быстро растёт. Поэтому можно сказать, что бозоны - “коллективисты”.
Интересный характер поведения имеет бозе-газ при  . Химический потенциал бозе-газа при
. Химический потенциал бозе-газа при 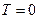 должен обращаться в нуль. В этом случае при приближении к абсолютному нулю числа частиц на квантовых уровнях
должен обращаться в нуль. В этом случае при приближении к абсолютному нулю числа частиц на квантовых уровнях 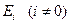 будут стремиться к нулю. Исключение составляют только частицы на нижнем квантовом уровне
будут стремиться к нулю. Исключение составляют только частицы на нижнем квантовом уровне  . Для числа частиц на энергетическом уровне
. Для числа частиц на энергетическом уровне  при
при 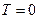 формула (3.8) приводит к неопределенному выражению
формула (3.8) приводит к неопределенному выражению  .
.
Таким образом, при приближении к абсолютному нулю бозе-частицы все более и более будут накапливаться на нижнем энергетическом уровне  и, наконец, все они окажутся на нем при
и, наконец, все они окажутся на нем при 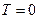 .
.
Это явление получило название бозе-эйнштейновской конденсации. Разумеется, такая «конденсация» не имеет ничего общего с конденсацией пара в жидкость.
2) Ферми-газ
В случае ферми-газа имеет место распределения Ферми – Дирака:
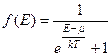 . (3.9)
. (3.9)
В отличие от (3.8), химический потенциал  в распределении (3.9) может иметь и положительное значение (в данном случае это не приводит к отрицательным значениям чисел
в распределении (3.9) может иметь и положительное значение (в данном случае это не приводит к отрицательным значениям чисел 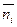 ).
).
График функции распределения Ферми – Дирака 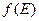 в случае
в случае 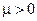 показан на рис. 3.6. При уменьшении энергии функция распределения Ферми-Дирака быстро принимает значение равное 1, т.е. среднее число фермионов в квантовом состоянии равно одному, что соответствует принципу Паули. Поэтому можно сказать, что фермионы - “индивидуалисты”.
показан на рис. 3.6. При уменьшении энергии функция распределения Ферми-Дирака быстро принимает значение равное 1, т.е. среднее число фермионов в квантовом состоянии равно одному, что соответствует принципу Паули. Поэтому можно сказать, что фермионы - “индивидуалисты”.
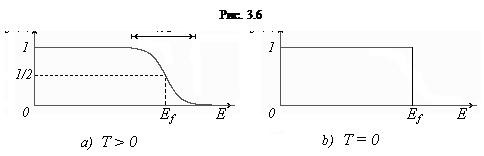
При абсолютном нуле температуры Т = 0

Это означает, что при Т = 0 частицы ферми-газа заполняют все квантовые состояния с энергиями 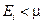 . Квантовые состояния с более высокими энергиями не заполнены. Говорят, что при Т = 0 ферми-газ находится в состоянии полного вырождения. Кривая, изображающая соответствующее распределение, вырождается в прямоугольник (рис. 3.6,б)
. Квантовые состояния с более высокими энергиями не заполнены. Говорят, что при Т = 0 ферми-газ находится в состоянии полного вырождения. Кривая, изображающая соответствующее распределение, вырождается в прямоугольник (рис. 3.6,б)
Таким образом, при Т = 0  совпадает с верхним заполненным электронным уровнем. Этот уровень называется уровнем Ферми или энергией Ферми
совпадает с верхним заполненным электронным уровнем. Этот уровень называется уровнем Ферми или энергией Ферми 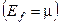 . Поэтому функцию распределения (3.9) можно ещё записать в виде:
. Поэтому функцию распределения (3.9) можно ещё записать в виде:
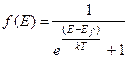 . (3.10)
. (3.10)
В заключение заметим, что функции распределения бозе-газа и ферми-газа отличаются только знаком перед единицей в знаменателе дроби, но этот знак приводит к принципиальным физическим различиям в области малых значений энергии, когда 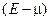 сравнимо с
сравнимо с 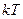 .
.
В случае же больших энергий, когда  (что выполняется в области “хвоста” кривых распределения) единицей в знаменателе можно пренебречь. Тогда обе функции распределения по состояниям с различной энергией принимают вид:
(что выполняется в области “хвоста” кривых распределения) единицей в знаменателе можно пренебречь. Тогда обе функции распределения по состояниям с различной энергией принимают вид:
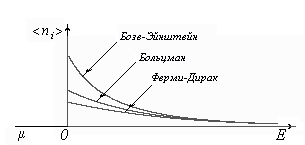 Рис. 3.7
Рис. 3.7
|
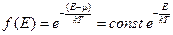 ,
,
т.е. переходят в классическое распределение Больцмана (см. рис. 3.7).
4. Внутренняя энергия твердого тела

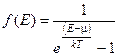 , (3.8)
, (3.8)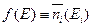 - среднее число частиц, находящихся в состоянии с номером
- среднее число частиц, находящихся в состоянии с номером 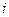 ,
,  – энергия частиц в этом состоянии.
– энергия частиц в этом состоянии. Значения химического потенциала
Значения химического потенциала  в распределении (3.8) не могут быть положительными, т.е.
в распределении (3.8) не могут быть положительными, т.е.  , ибо в противном случае при
, ибо в противном случае при  среднее число
среднее число 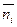 оказалось бы отрицательным.
оказалось бы отрицательным. График функции распределения Бозе-Эйнштейна в случае
График функции распределения Бозе-Эйнштейна в случае 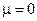 для температуры
для температуры  представлен на рис. 3.5.
представлен на рис. 3.5. . Химический потенциал бозе-газа при
. Химический потенциал бозе-газа при 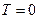 должен обращаться в нуль. В этом случае при приближении к абсолютному нулю числа частиц на квантовых уровнях
должен обращаться в нуль. В этом случае при приближении к абсолютному нулю числа частиц на квантовых уровнях 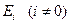 будут стремиться к нулю. Исключение составляют только частицы на нижнем квантовом уровне
будут стремиться к нулю. Исключение составляют только частицы на нижнем квантовом уровне  . Для числа частиц на энергетическом уровне
. Для числа частиц на энергетическом уровне  .
.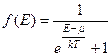 . (3.9)
. (3.9)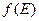 в случае
в случае 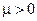 показан на рис. 3.6. При уменьшении энергии функция распределения Ферми-Дирака быстро принимает значение равное 1, т.е. среднее число фермионов в квантовом состоянии равно одному, что соответствует принципу Паули. Поэтому можно сказать, что фермионы - “индивидуалисты”.
показан на рис. 3.6. При уменьшении энергии функция распределения Ферми-Дирака быстро принимает значение равное 1, т.е. среднее число фермионов в квантовом состоянии равно одному, что соответствует принципу Паули. Поэтому можно сказать, что фермионы - “индивидуалисты”.

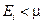 . Квантовые состояния с более высокими энергиями не заполнены. Говорят, что при Т = 0 ферми-газ находится в состоянии полного вырождения. Кривая, изображающая соответствующее распределение, вырождается в прямоугольник (рис. 3.6,б)
. Квантовые состояния с более высокими энергиями не заполнены. Говорят, что при Т = 0 ферми-газ находится в состоянии полного вырождения. Кривая, изображающая соответствующее распределение, вырождается в прямоугольник (рис. 3.6,б)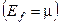 . Поэтому функцию распределения (3.9) можно ещё записать в виде:
. Поэтому функцию распределения (3.9) можно ещё записать в виде: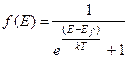 . (3.10)
. (3.10)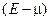 сравнимо с
сравнимо с 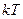 .
. (что выполняется в области “хвоста” кривых распределения) единицей в знаменателе можно пренебречь. Тогда обе функции распределения по состояниям с различной энергией принимают вид:
(что выполняется в области “хвоста” кривых распределения) единицей в знаменателе можно пренебречь. Тогда обе функции распределения по состояниям с различной энергией принимают вид: Рис. 3.7
Рис. 3.7
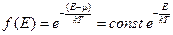 ,
,


