Внутренняя энергия и теплоемкость кристалла. Закон Дебая
С учетом (4.12) внутренняя энергия кристаллического твердого тела равна
где Возьмем один моль вещества, тогда N = NA, и производная от U по T даст молярную теплоемкость кристалла:
Величину θ, определяемую условием
Температура Дебая указывает для каждого вещества ту область, где становится существенным квантование энергии колебаний. Введем также переменную
где Запишем также в этих обозначениях выражение для внутренней энергии кристалла
В общем случае вычисление интегралов в выражениях (4.16) и (4.17) представляет большую трудность, однако, существуют два предельных случая, где вычисление их возможно. 1) При Т << θ верхний предел интеграла в (4.17) будет очень большим, так что его можно приближенно положить равным бесконечности (x max ≈ ∞). Тогда этот интеграл будет представлять собой некоторое число, а именно
Внутренняя энергия U в этом случае будет равна:
а молярная теплоемкость окажется пропорциональной кубу температуры:
Эта приближенная зависимость известна как закон Дебая. При достаточно низких температурах этот закон выполняется во многих случаях очень хорошо. 2) При T >> θ, т.е. при
Тогда для внутренней энергии получается выражение:
а для молярной теплоемкости значение
фигурирующее в законе Дюлонга и Пти. Рассмотренные случаи согласуются с графиком зависимости теплоемкости кристалла от температуры, показанным на рис. 4.1. Формула Дебая (4.18) хорошо передает ход теплоемкости с температурой для тел с простыми кристаллическими решетками, т.е. для химических элементов и некоторых простых соединений.
Литература 1. Савельев И.В. Курс общей физики. – М.: Наука, т. 2, 1989. 2. Сивухин Д.В. Общий курс физики. – М.: Наука, т. 2, 1990. 3. Матвеев А.Н. Курс общей физики. - М.: Высшая школа, т. 2, 1976-1989. 4. Верещагин И.К., Кокин С.М., Никитенко В.А., Селезнев В.А., Серов Е.А. Физика твердого тела. - М., Высшая школа, 2001.
|

 , (4.13)
, (4.13) – энергия нулевых колебаний атомов в кристалле.
– энергия нулевых колебаний атомов в кристалле. . (4.14)
. (4.14) , называют характеристической температурой Дебая. По определению
, называют характеристической температурой Дебая. По определению . (4.15)
. (4.15) . Тогда выражение для теплоемкости примет вид:
. Тогда выражение для теплоемкости примет вид: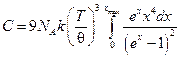 , (4.16)
, (4.16) .
. . (4.17)
. (4.17) .
.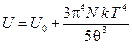 ,
, . (4.18)
. (4.18)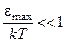 , формулу (4.13) можно упростить, положив
, формулу (4.13) можно упростить, положив .
. ,
, , (4.19)
, (4.19)


