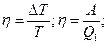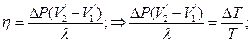АвагадроШарля - изобарный V=V0(1+αt), при P = const.
Гей – Люссака – изохорный
P = P0(1+αt), при V = const. Все законы при m = const. Авагадро Моли любых газов при одинаковых темпер-е и давл-ии занимают одинаковые объёмы. При н.у. этот V=22,41*10-3 м3/моль. В одном моле различных веществ содержится одно и то же число молекул: NA = 6.022*1023 моль-1. Дальтона Давление смеси идеальных газов равно сумме парциальных давлений P1,P2,…,Pn входящих в неё газов: P = P1+P2+….+Pn. Парциальное давление – давление, кот-е производил бы газ, входящий в состав газовой смеси, если бы он один занимал объём, равный объёму смеси при той же темпер-ре. Уравнение Клапейрона-Менделеева. Необходимо получить связь между нач. и кон. состояниями газа. 1) P1,V1,T1; 1→1’(T1=const)
2)P2,V2,T2. По газ. законам: P1V1=P1’V2
Т.о. B – газовая постоянная. m = μ;V=V0; Возьмём массу газа = 1 моль→ R – универсальная газовая постоянная = 8,31 (Дж/моль*К). Ф/с R – та работа, которую сов-т 1 моль газа при нагревании на 1 К. Для любого объёма:
№2.Реальный газ. Уравнение изотермы В-д-В. З соответст состояний Не,Н2. PV=RT – осн. ур-е опис. состояние идеал газа. Высокая Т и низкое Р – условие, при кот можно использовать ур-ние М-К для опис реал газов. r~10-10м p0=1атм, Т=273 К. Na=2,7·1025м-3(число Лошмидта) V=Nл·N0=2,7*1025*4*10-30=10-4м3 Доля суммарного объема V/1м3=0.0001 P0=3 атм, доля суммарного объема повысится в 3 раза. Молекулы реальных газов не могут сблизиться, взаим происходит на расстоянии, т.е доля суммарного объема всех молекул будет возрастать очень быстро. Это и нужно учитывать при составлении Ур. М-К. Между молекулами реал газов сущ очень сильное взаимодействие: притяжение, отталкивание. Это все обусловлено внут энергией взаимод-их ядер. r0 – соот равновесному состоянию системы. Силы отталк. И притяжения равны. d-мин. Расстояние до кот могут сблизиться атомы, кин энергия падает и переходит в потенциальную. Уменьшается V появл. внутр.Р. отличие реальных газов от идеальных заключ в конеч. размерах молекул газа, так что при опред условиях нельзя принебрегать суммарным объемом молекул. Взаимодействие между молекулами, кот приводит к дополнит внутр или межмол-му давлению. Поэтому реал газ при данных условиях занимает как-бы меньший объем и находится под большим давлением Уравнение Ван-Дер-Ваальса PV=RT – Ур-ние М-К для идеал газов (V-b)(P+P|)=RT, где P|-определяет взаимодействие между молекулами, b-учитывает размеры молекул P|=a/V2, a-1ая поправка Ван-дер-Ваальса учитывающ взаимод между молекулами.
b=4V0n, b-учетверенный объем всех молекул заключ в единице объема
Изотермы Ван-Дер-Ваальса
К- критич точка, соот P и V критич. – выше идет изотерма В-д-В Критические параметры и их связь с постоянными В-д-В
Выразим P
Условие при кот-м произ=0: V=Vkp; P=Pkp; T=Tkp
Возьмем уравнение М-К для Крит параметров Pkp*Vkp=RTkp;
Закон соответственных состояний: Закон соответственных состояний гласит, что все вещества подчиняются одному уравнению состояния, если это уравнение выразить через приведенные переменные. Для каждого газа критические парметры разные (темпер., давление, объем) àразные параметры газа (а,в) в ур-ие Ван-дер-Вальса. Т.к.для хар-ки поведения газа важно не столько абсолютное значение параметров сост-я, сколько относительное(в долях крит пар-в)
ур-ние В-д-В преобраз.след.образом: à Любому состоянию любого газа можно поставить соответствие, з-я p,V,T и крит. р,V,T можно рассчитать Т.№3. Понятие внутренней энергии и температуры. Внутренняя энергия идеального газа. Теплота и работа. Первый закон термодинамики и его применение к процессам в идеальном газе. Температура – физический параметр, который одинаков во всех частях системы тел, находящихся в состоянии теплового равновесия. (Др.словами, температура – характ-т сост-ие термодин-го равновесия макроскоп-й системы.) Тело, как система состоящая из мк частиц, обладает внутренней энергией. С позиции МКТ внутренняя энергия – это сумма потенциальной энергии взаимодействия частиц (молек.притяг. и отталкив.), составляющих тело, и кин.эн-ии их беспорядочного теплового движения. Т.к. кин.эн-ия беспорядочного движения ~T, потенциальная эн-ия взаимодействия зависит от расстояния м/у частицами, т.е. от V тела. Поэтому в термодинамике внутр.эн-я U определяется как функция его макроск-их параметров. (p, T, V) Изменить внутр.эн-ию можно 2-мя способами:1) совершением мех.работы; 2)теплопередачей. При изменении внутр.эн-ии посредством совершении мех. работы, т.е. при мех.взаимод-ии данного тела с др.телам, мерой энергии служит работа A. Совершение работы – Aсовершения работы над телом или самим телом называется теплопередачей. Теплопередача-это микроскопический способ передачи эн-ии, п-ри этом мерой переданной эн-ии является количество теплоты Q. Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии: Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Внутренняя эн-ия ид.газа: Если потенциальная эн-ия взаимодействия равна 0, внутренняя энергия идеального газа равна сумме кин.эн-ий хаотического теплового движения молекул: Для 1ат. газа: степень свободы = 3(только поступательное движение(3 направления)), 2 ат.газа i=5(поступ.дв-е (3 направления) +вращательное в 2-ч плоскостях), 3ат. И многоатомные i=6 (п).оступ.дв-е+вращ.дв-е+колебательное дв-е Внутр.эн-ия идеального газа прямо пропорциональна его абс.температуре (при изм-ии Т изменяется и U, если Т=const, то U –не изменяется). Работа: Рассмотрим газ находящ.в цилинд-ом сосуде под поршнем, газ действует на поршень с силой F =pS (где р-давление газа, S- площадь поршня). Если поршень при этом перемещается, то газ совершает работу. При расширении газа эта работа будет +, при сжатии работа газа будет -.
Работа газа в произвольном процессе: Рассмотрим малое изменение объёма dV, настолько малое что р можно считать постоянным. Газ совершает малую работу
Первое начало термодинамики (закон сохранения эн-ии): Энергия не исчезает и не возникает из не от куда, она лишь преобразуется из одной энергии в другую, передается от одной системы (тела) к другой. (Др.формулировки: Термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Существование вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, невозможно. Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил.) Т.о. приращение внутр.эн-ии системы должно быть = сумме совершенной над системой работой A` и количества сообщенного системе тепла Q: Обычно вместо А` (работы, соверш.внешн.силами) рассма-ют А(работу, совершаемую стстемой над внешними телами и равную –А`). Тогда, Q = U2-U1+A. При вычислении совершенной системой работы или полученного системой тепла обычно приходиться разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из кот.соответствует весьма малому изменению параметров системы. Тогда, получаем: Применение 1 начала термодинамики к процессам в ид.газе: 1) при V=const (изохорный проц-с) тог да
Т.№4. Второй закон термодинамики. Цикл Карно и его к.п.д. Обратимые и необратимые циклы, их к.п.д. Приведенное количество теплоты, неравенство Клаузиуса. Технические циклы, тепловые машины. Идея 2го з-на термодинамики связана с именем француз-го инженера Сади Карно, кот.в 1824г.разработал цикл Карно-круговый процесс в тепловой машине, в рез-те кот-го тело, совершив работу, возвращается затем в исходное состояние, используя часть этой работы. Он впервые показал, что полезную работу можно получить лишь в случае, когда тепло передается от нагретого тела к более холодному. Второй з-н Термодинамики: во 2ом н.термодинамики говорится о направлении, в кот.происходит превращении энер-ии. Согласно 2ому началу, во-первых, превращение теплоты в работу возможно только при наличии холодильника и нагревателя; во-вторых, в тепловых машинах полезно используется только часть энергии, передаваемая от нагревателя к холодильнику (матем.это выражается кпд идеальной тепловой машины). Формулировки: 1) Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния S=S(T,..), называемая энтропией, такая, что ее полный дифференциал Цикл Карно: круговой тепловой процесс, в рез-те кот-го некоторое количество теплоты переносится от горячего тела к холодному в идеальной тепловой машине.(Круговой процесс, состоящий из двух изотерм и двух адиабат.) (Сх. тепловой машины:1-нагреватель, 2-холодильник, 3 – рабочие тело.) Рабочие тело (газ, …) под действием нагрева-ля будет изотермич.расшир-ся, поглощая Q1 (на графике процесс 1-2) 1→2 (T1=const) Q1>0; A12>0, A12 = Q1. Далее рабочее тело подвергается адиабатическому расширению без теплообмена с окружающей средой (процесс 2-3), на этом участке тело совершает работу за счет своей внутренней энергии (A23 > 0). При последующем изотермическом сжатии (процесс 3-4) холодильник забирает у рабочего тела теплоту Q2. (A34 < 0 и отдает тепло Q2 < 0, A34=Q2). Процесс 4-1 представляет собой адиабатическое сжатие, переводящее рабочее тело в первоначальное состояние. (Газ совершает работу A41 < 0.) Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках: A = A12 + A23 + A34 + A41.
На диаграмме (p, V) эта работа равна площади цикла. Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газа A = –ΔU = –CV (T2 – T1), где T1 и T2 – начальная и конечная температуры газа. Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам A23 = –A41. Тепловой коэффициент полезного действия (к.п.д.) цикла любой тепловой машины можно рассчитать как отношение полезной работы к количеству теплоты, переданной от нагревателя. Тогда, КПД цикла Карно: Обратимый процесс: - это процесс, при завершении которого система возвращается в первоначальное состояние, при этом в первоначальное состояние возвращаются все взаимодействовавшие с ней тела. Обратимый процесс характеризуется бесконечно медленным изменением термодинамических параметров (плотности, давления, температуры и др.), определяющих равновесие системы. Необратимый процесс: процессы, которые могут самопроизвольно протекать только в одном определённом направлении. Все реальные процессы необратимы. Пример необр цикла – расширение газа в пустоту.→молекулы никогда сами не собирутся в объеме; процессы диффузии. Приведенное количество теплоты: Отношение теплоты Q, которое получило тело в изотермическом процессе, к температуре Т теплоотдающего тела. Приведенное количество теплоты, которое сообщается телу на малом участке процесса, равно δQ/T. Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе, равно нулю: Из равенства, взятого по замкнутому контуру, следует, что подынтегральное выражение δQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, которым система пришла в это состояние. Таким образом, Технические циклы:
Тепловые машины Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами. №5. Понятие энтропии, термодинамическое и стат опр-е энтропии.
Применим нер-во Клазиуса:
Разобъем интеграл
Интеграл не зависит от формы пути, след-но подинтег выр-ние есть ф-ия состояния, она наз-ся энтропией
Q/T=ΔS, чем выше темп-ра нагр-ля, тем ниже изм-е энтропии В тепл машине: чем ниже ΔS раб в-ва, тем выше кпд и чем выше ΔS, тем ниже кпд, ниже работоспособность, т.е. энтропия асоц с работоспособностью. Стат смысл: чем больше энтропия, тем больше вер-ть события Т.о для обратимого процесса изм-е энтропии равно 0 (ΔS=0(*)), т.е если ΔS=0, то цикл обратимый. Энтропия системы, сов-щей необратимый цикл, возрастает: ΔS>0 (**) Выр-ния (*) и (**) относятся только к замкнутым системам, если же система обменивается теплотой с внеш средой, то ее энтропия м вести себя любым образом. Рассм замкнут процесс: одна ветвь nb1 обратима, а другая 1ап необратима, т.е в целом цикл необратим.
1-е н.т/д: dQ=dU+dA=dU+pdV (1) 2-е н.т/д: dS=dQ/T (2) Подставим 1-е во 2-е: dS=(dU/T)+(pdV/T) (3) dU=CVdT pV=RT pdV=RdT (при p=const) dSp=(CVdT/T)+(RdT/T) В общем случае: выразим из М-К p: p=RT/V
Проинтегрируем: S=CVlnT+RlnV+S0 или V=const ΔSV=CVlnT2/T1 T=const ΔST=RlnV2/V1 P=const ΔSP=CVln(T2/T1)+RlnT2/T1=CPlnT2/T1 Адиаб. dQ=0; ΔS=dQ/T>=0 обр процесс т.е S=const Все урав-ния м переписать исп-я энтропию или внут энергию, т.к это ф-ции состояния (1) V=const dS=CVlnT2/T1; S=CVlnT+lnS0
2.Цикл Карно
2 изотер || 3. T1>T2
I: ΔS1=-Q/T1(выдел-т тепло) II: ΔS2=Q/T2(погл тепло)
ΔS= ΔS1+ ΔS2=(-Q/T1)+(Q/T2)=Q(1/T2-1/T1)=Q(T1-T2./T1T2)>0, Но T1>T2 след-но ΔS>0. Более глубокий смысл энтропии раскрывается в стат физике: Энтропия связывается с т/д вероятностью сост системы. Т/д вероятность – число способов, кот-ми м/б реализовано данное сост-е макроскоп системы, или число микросостояний осущ данное макросостояние Согласно Больцману: S=klnW-мера неупорядоченности системы (где k-пост Больцмана) Чем больше число мкросостояний, реализующих данное макросост, тем больше энтропия. Т.к реал процессы необр, то м утверждать, что все процессы в замк системе ведут к увеличению ее энтропии – принцип возрастания энтропии
Т. №6 Функция распределения молекул по скоростям. Распределение максвелла и его свойства Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной. Пусть в единице объема n молекул. Какая доля молекул Основываясь на опыте Штерна, можно ожидать, что наибольшее число молекул будут иметь какую-то среднюю скорость, а доля быстрых и медленных молекул не очень велика. Необходимые измерения показали, что доля молекул
Функция распределения молекул по скоростям или закон Максвелла.
где m – масса молекулы, k – постоянная Больцмана. Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема. Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул. Она рассчитывается по формуле:
Сопоставляя все три скорости: 1) наиболее вероятную 2) среднюю 3) среднюю квадратичную
Максимум кривой будет смещаться вправо при повышении температуры и влево при понижении температуры. Высота максимума не будет оставаться постоянной. Площадь заштрихованной фигуры численно равна доле
Выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение может быть записано в виде:
где р — давление на высоте h. Выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести. Т.№8Понятие о степенях свободы мол-л и теорема о равномерном расп-ии энергии по степеням свободы. Классич теория теплоемкости газов и тв тел. Закон Дюлонга-Пти. Понятие о «замороженных» ст. свободы. Адиаб процесс. Ур-ие адиабаты. Число степеней свободы – число независимых переменных(коор-т), полностью опред-х полож-е сис-мы в пр-ве. В ряде задач мол-лу 1-атомного газа рассм как мат точку, кот приписывают 3 степени свободы пост. дв-ия. Вкласс мех-ке мол-ла 2-атомного газа в 1-м приближении рассм как совок-ть 2х мат точек, жестко связанных недеформ связью. Эта сис-ма кроме 3-х ст свободы пост движения имеет еще 2 ст своб. вращ движ-я. Т.о 2х-атомный газ обл-т 5-ю степенями свободы (i=5). Трехатомная и многоатомная нелин мол-лы 6 ст свободы: 3-пост и 3-вращ. Реально жест связи между мол-ми не сущ-ет поэтому необходимо учитывать степени свободы колеб движ-я. Независимо от общего числа ст св молекул 3 степени всегда пост Ни одна из пост ст свободы не имеет преимущества перед другой, поэтому на каждую из них приходитсяв среднем одинаковая энергия, равная 1/3 зн <E0> в формуле <E0>=(3/2)kT – средняя кин энергия пост движ-я одной мол-лы <E1>=<E0>/3=(1/2)kT В класс стат физике выводится з Больцмана о равномерном распред-и энергии по степеням свободы мол-л: для стат сис-мы, нах-ся в сост-и т/д равновесия, на каж-й пост и вращ ст свободы приходится в ср.кин энергия = kT/2, а на каж колеб, энергия=kT Колеб степень обладает вдвое большей энергией потому, что на нее прих-ся не только кин энергия но и пот энергия причем их значения одинаковы. Т.о ср энергия мол-лы: <E>=(i/2)kT (i- сумма числа пост, вращ, и удвоен числа колеб степ свободы) Т.к в идеальном газе взаимная пот энергия = 0, то внут энергия NA молекул:Um=(i/2)kTNA=(i/2)RT (1моль); U=(m/μ)(i/2)RT=ν(i/2)RT Теплоемкость – физ вел-на, хар-ая какое кол-во теплоты необх чтобы нагреть тело на 1 град. СТЕЛА=Дж/град Уд теплоемкость – кол-во теплоты необх для нагревания ед массы на 1 кельвин: СУД=Дж/кгК Мол теплоемкость: СМОЛЬ=Дж/мольК СУД=СМОЛЬ/μ=СТЕЛА/m cm – теплоемкость тела Q=cm(t2-t1)=CТЕЛА(t2-t1) dQ=CdT, след-но С=dQ/dT Для газа небезразлично то условие при кот происходит нагревание. Различают нагревание при P=const и V=const и теплоемкости будут различны. CP,CV – молярные теплоемкости V=const. Все тепло идет только на нагревание, т.е изменение внут энергии. ΔQV=ΔU U=(i/2)RT, след-но ΔU=(i/2)RΔT ΔQV=(i/2)RΔT; CV= ΔQV/ΔT= (i/2)R P=const. QP=ΔU+ΔAP тепло идет на нагревание и совершение работы ΔAP=RΔT ΔQP=(i/2)RΔT+RΔT=(i/2R+R) ΔT=((i+2)/2)RΔT CP=((i+2)/2)R CP/CV=(i+2)/i=γ – показатель адиабаты -)С не зависит от темп-ры, для каждого газа постоянна При абсолютной Т, С→0 Уменьшение С при уменТ ведет к уменьш числа степеней свободы (т.е замороженные степени свободы) -)Закон Дюлонга и Пти: атом теплоемкость простых хим веществ постоянна и равна 3R и не зависит от температуры. Выполняется при дост выс. Т, характерно для каждого в-ва. Каждая составляющая крист решетку ч-ца имеет 3 колеб степени свободы, на каждую приходится энергия кТ Um=3NAkT=3RT; CV=dUm/dT=3R=25Дж/мольК Для хим соединений CV=3nR=25n Дж/мольК Адиабатический процесс – процесс, кот происходит без обмена теплом с окр средой На практике: изотермич процесс нужно проводить очень медленно Адиабат процесс протекает очень быстро и все процессы, кот в природе протекают быстро приближенны к адиабатич. dQ=dU+dA (1) dQ=0; U=CVT; dU=CVdT; dA=pdV 0=CVdT+pdV (2) pV=RT, след-но p=RT/V 0=CVdT+RTdV/V lnT+(R/CV)lnV=const lnT+lnVR / Cv=const ln(TVR / Cv)=const TVR / Cv=const| R/Cv=(Cp-Cv)/Cv=γ-1 след-но TVγ-1=const T1/T2=(V2/V1)γ-1 T=pV/R pVVγ-1=const| pVγ=const – уравнение Пуассона – описывает процесс P1/γV=const; V=RT/P;
Изотермический процесс: PV = const;
dP/dV=-P/V; PVγ=const – адиаб. VγdP+γPVγ-1dV=0 Vdp+γPdV=0
У адиабаты угол наклона больше.
Т.№9. Хар-р теплового движ-я мол-л и св-ва в-ва в разл. агр-х сот-х. Основной моделью МКТ явл-ся совок-ть диж-ся и взаим-х м/у собой мол-л вещ-ва. Взаимное распол-е, хар-р движ-я и взаим-я мол-л, сущ-о зависит от внеш-х усл-й (Т, Р), характ-т его агрег-е сост-е. Различают 4 АС: Т,Ж,Г,Плазменное. Фаз. Переход – переход сист-ы из одного АС в другое. Реализация того или иного АС зав-т от сост-я кин. и пот энергии мол-л. Тв.тело – вещво нах-ся в тв. сост-ии, если ср. пот. энергия прит-я мол-л >> их ср. кин-й энергии. Каждая мол-а занимает определ-й Vпрос-ва, притягивая сосед. молекулы и одновр. отталк-я их, не давая занять своё место. Ч-цы кол-ся около нек-х ср-х положений равновесия – узлы кр.р. Тв.тела сохраняют форму объём. Жидкость: при нагревании ↑ кин. эн-я, ↑ амплитуда кол-я, ↓ эн-я связи мол-л →нарушение дального порядка. Фаз переход: Т→Ж. Частицы кол-ся в большой области, пол-я равн-я подвижны. Ср. кин. энергия мол-л соизмерима со ср. пот. энер. их притяжения. Ближний порядок Ж течёт и принимает форму сосуда. Текучасть объясняется тем, что мол-лы дв-ся в напр-ии дейст-я внеш-й силы. Газ – ср.кин.энергия > ср.пот.энергии. М. неограниченно расширятся в пространстве. Сжимаемость объясн-ся межмолек-м пространством. Мол-лы движ-ся по прямолинейным траект-м, столкн-я измен-т напр. Плазма: ↑T, ↑ кин.эн. →деф. эл-х оболочек и выбивание е-в из атомов. Состав газа – мол-лы и заряж-е частицы, заряд не измен-ся, т.о. это электронейтральная совокупность нейтральных и заряженных час-ц. Фаза. Физ. однородное тело, занимающее опред-й объём. В пределах одного АС вещ-о м. нах-ся в неск-х фазах, отличающ-ся по своим свой-м, составу и строению. (лёд м. нах-ся в 5 фазах). Переход в-ва из одной фазы в другую – фаз-й переход- изм-е св-в вещ-ва. Фаз-й переход I рода(плавл.,кристалл-я) сопр-ся поглощением или выделением теплоты, хар-ся постоянством t, изм-ми S и V/ Фаз-й переход II рода – не связаны с поглощением или выделением теплоты и измен-м V. Хар-ся пост-м V и S, но скачкообр. изменением теплоёмкости. 2 фазы м. находиться при непосредственном соприкосновении, они находятся в равновесии. P,T – равновесные в данном состоянии. В равновесии м. нах-ся не более 3х фаз. Р=Р(Т) – функция от температ-ры. Диаграмма фазовых состояний.
Уравнение Клапейрона-Клаузиса. Термод-ка даёт метод расчёта кривой равновесия 2х фаз одного и того же вещ-ва.
АБ – испарение ВС – адиаб-е расш-е(парообр-е) СД – конденсация
Q1=ΔQ=λm1 – подвели. λ – теплота фаз. перехода. A=ΔP(V2- V1)= ΔP m1(V2’- V1’) Ρ=m/V=mV’ – уд. объём.
|
α-термич. коэфиц-т объёма. α=1/273(1/град).
1’)P1’;V2,T1; 1’→2(V2=const)
- уравнение Клайперона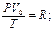
(Менделеев обобщил уравнение Клайперона для любой массы)
Уравнение В-д-В для 1 моля
Уравнение В-д-В для любого кол.
если К- точка перегиба, то 1-ая 2-ая произв. Обращаются в 0.
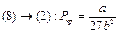__(9)
Т.е вещество не подчиняется Ур-нию М-К
, 
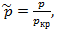
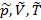. Зная p,V,T второго газа можно найти его крит. р,V,T.
.
, где М – молярная масса, m –масса газа, R – универсальная газовая постоянная, T – абсолютная температура, i-степень свободы.
Работа газа в изобарном процессе: Предположим, что газ расшир-ся при постоянном давлении. Тогда сила, с кот.газ действует на поршень тоже постоянна. Пусть поршень переместился на расстояние 
Работа газа будет равна: 
Если V1 и V2 – нач. и конечн.объем газа, то А = р(V2-V1).
Изобразив данный процесс на диаграмме pV, мы видим что работа = площади прямоугольника под графиком. (Если предположить, что газ сжимается, то A= -p(V1-V2)=p(V2-V1).)
Тогда работа газа во всем процессе найдется суммированием этих малых работ. 
Работа при переходе из одного состояния термодинамической системы в другое: В зависимости от траектории I или II перехода из первого состояния во второе, площадь под кривой р(V) будет различна, а, следовательно, будет различна механическая работа, совершаемая системой в этих термодинамических процессах.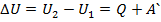
, где U1 и U2 – начальное и конечное значения внутр.эн-ии.
, но т.к. внутренняя эн-ия явл-ся функцией состояния и имеет вполне определенное значение и не зависит от пути перехода системы из состояния 1 в 2, то 
à 
. (А и Q – зависят от пути перехода системы из состояния 1 в 2; они не явл-ся функц-ми состояния.)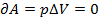
à 
2) при p=const (изобарный процесс) 
. 3) T=const (изотермический процесс), тогда 
. Для 1 моля газа ур-е сост-я ид.газа: pV=RTà p=RT/V à 
à 
4) адиабатиче-ий процесс - термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством. 
.
.2) Томсона: Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара. 3) Клаузиуса: Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему. 4) вечный двигатель 2го рода невозможен. (Машина, которая, будучи пущена в ход, превращала бы в работу всё тепло, извлекаемое из окружающих тел.) 
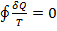. (1) (интеграл Клаузиса)
. Функция состояния, у которой дифференциал равен δQ/T, называется энтропией и обозначается S. Из формулы (1) следует, что для обратимых процессов изменение энтропии 
. В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает: 
. Выражения (3) и (2) применяются только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя произвольным образом. Соотношения (2) и (3) можно представить в виде неравенства Клаузиуса: 
, т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов). Для необратимых процессов: 
à 
.
- Термодинамический цикл прямоточного воздушно-реактивного двигателя.
- Термодинамический цикл двигателя внутреннего сгорания.
- Циклы дизельного двигателя.
Рассм замкн цикл, каждая ветвь кот-й обратима, след-но весь цикл обратим, т.е происходит без внеш воздействия.
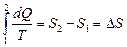Физ смысл(мера неработоспособности): Q/T – получает раб в-во от нагревателя при данной темп-ре, если темп-ра нагр увел, то кпд увел.
;
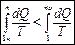В необр процессе энтропия возрастает, след-но ΔS>=0, т.е в необр процессе она возр
осн ур-е тер-дин-ки
2 адиаб =
имеет скорости от v 1 до v 1 + Δ v? Это статистическая задача.
, отнесенная к интервалу скорости Δ v, т.е.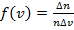 
, имеет вид, показанный на рис. 3.3.
– (смысл) вероятность того, что молекулы имеют скорость в данном интервале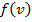 
.
– условие нормировки функции распределения на единицу (т.е. площадь фигуры на предыдущем рисунке=1)
или 
,
,
, – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная. Относительное число быстрых и медленных молекул мало (рис. 3.4).
общего числа молекул n, которую образуют молекулы со скоростями в указанном интервале. Общая площадь, ограниченная кривой распределения и осью абсцисс (скоростей), таким образом, равна единице и не меняется при изменении температуры (рис. 3.5).
Поэтому высота максимума меняется при изменении температуры.
Т.№7. Распределение молекул в силовом поле. Барометрическая формула. Распределение Больцмана в случае дискретных значений энергии. 
. 
где mgh — П — потенциальная энергия молекулы в поле тяготения.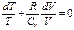
pdV+VdP=0;
- Ур-е адиабаты.
Для наглядного изобр-я фаз. превращения. В коор-х Р,Т задаётся зав-ть м/у t фаз. перехода и давления в виде кривых испарения (КИ), плавления(КП) и сублимации(КС) – из пара в ТВ. сост-е, разделяют на области: ТТ,Ж и Г фаз. Каждая точка на кривых фаз равновесия соот-т усл-м равн-я 2х сосуществ.фаз:КП-ТТ и Ж; КИ-Ж и Г; КС-ТТ и Г. Точка в кот-й они пересекаютя – тройная точка – одновр-е сущ-е 3х фаз вещ-а в равновесии. Каждое в-во имеет такую точку. Для воды 273,15 К.
М. установить зав-ть между Р и Т фаз. перехода используя метод циклов.
