№60
То же что и 59 вопрос
№61
При расчете надежности РЭА по постепенным отказам определяется вероятность попадания выходного определяющего параметра РЭА Y в пределы допуска [ Y 1; Y 2]. Для этого прежде всего необходимо знание уравнения связи, определяющего вид зависимости определяющего параметра Y от параметров элементов и конструкции РЭА x i:
 . (26)
. (26)
Исходными данными для расчета надежности по постепенным отказам являются:
– характер постоянного изменения математического ожидания каждого параметра конструкции  , например, от температуры
, например, от температуры  или времени эксплуатации
или времени эксплуатации  ;
;
– среднее квадратическое отклонение параметров конструкции, вызванное дестабилизирующими случайными факторами технологического процесса, условий эксплуатации, временем  ;
;
– допуск на определяющий параметр [ Y 1; Y 2]. Предполагается, что функция распределения случайных величин параметров конструкции является гауссовской, т. е.
 , (27)
, (27)
причем в нормальных условиях эксплуатации математическое ожидание  совпадает с номинальным значением
совпадает с номинальным значением  .
.
Где пункт 1?
2. Из (26) получают уравнение абсолютной погрешности определяющего параметра
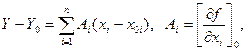 (28)
(28)
где индекс «0» означает, что в выражение для A i подставляются номинальные значения параметров конструкции.
3. Определяются математическое ожидание МY и среднее квадратическое отклонение σY определяющего параметра при заданных температуре или сроке эксплуатации:
 (29)
(29)
где  – коэффициент корреляции случайных величин x i и х j.
– коэффициент корреляции случайных величин x i и х j.
4. Определяется вероятность работоспособности устройства в предположении, что функция распределения плотности вероятности случайной величины определяющего параметра является гауссовской:
 (30)
(30)
№62
На поле мужик, запряженный в плуг, пытается пахать. Идет по скользкой грязи, тащит плуг, падает лицом в грязь, встает и снова падает. И так без конца.
Вдоль поля по дороге едет дорогая иномарка и внезапно останавливается недалеко от мужика. Опускается стекло и из салона раздается:
- Экскьюз ми, ду ю спик инглиш?
На что мужик:
- Йес, ай ду, а хули толку?
№63 Теорема гипотез дает возможность пересматривать принятое первоначально решение о вероятностях появления интересующих нас событий в зависимости от поступившей дополнительно информации. Байесовские методы позволяют включать ранее известные знания, убеждения и информацию, помимо тех, что содержатся в наблюдаемых данных, в процесс вывода. Сюда могут включаться данные из предыдущих исследований, известные характеристики используемой модели, и другие объективные или субъективные источники данных.
Вероятности, характеризующие суждение человека о будущих событиях до получения дополнительной информации, называются априорными.
Вероятности, пересмотренные после получения дополнительной информации, называются апостериорными.
Формула Байеса записывается следующим образом:
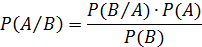
где P (A)—априорная вероятность гипотезы А,  — вероятность
— вероятность  гипотезы A при наступлении события B (апостериорная вероятность), — вероятность наступления события B при истинности гипотезы A, P (B) — вероятность наступления события B.
гипотезы A при наступлении события B (апостериорная вероятность), — вероятность наступления события B при истинности гипотезы A, P (B) — вероятность наступления события B.
№64 Если событие А может произойти только при выполнении одного из событий  , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
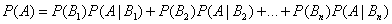 .
.
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий  , вероятности появления которых
, вероятности появления которых  . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий  , которые будем называть гипотезами. Тогда по формуле полной вероятности
, которые будем называть гипотезами. Тогда по формуле полной вероятности
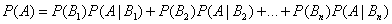
№65 Если событие А произошло, то это может изменить вероятности гипотез  .
.
По теореме умножения вероятностей
 ,
,
откуда
 .
.
Аналогично, для остальных гипотез
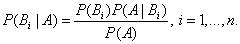
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез 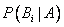 называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как 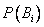 - априорными вероятностями.
- априорными вероятностями.
|
| Априорные методы расчета надежности.
|
|
| Виды технического состояния объектов.
|
|
| Дискретные случайные величины. Ряд распределения. Кумулятивная кривая.
|
|
| Законы распределения вероятностей дискретных случайных величин.
|
|
| Законы распределения вероятностей непрерывных случайных величин
|
|
| Испытания на надежность. Виды испытаний на надежность.
|
|
| Испытания на надежность. Организация обработки первичной документации
|
|
| Испытания, основанные на накоплении информации о надежности. Второй случай
|
|
| Испытания, основанные на накоплении информации о надежности. Первый случай
|
|
| Испытания, основанные на накоплении информации о надежности. Теорема гипотез.
|
|
| Испытания. Цели испытаний. Классификация испытаний.
|
|
| Количественные показатели надежности восстанавливаемых изделий. Вероятность
|
|
| Количественные показатели надежности восстанавливаемых изделий. Поток отказов
|
|
| Комплексные показатели надежности восстанавливаемых изделий. Функция
|
|
| Композиция и суперпозиция законов распределений случайных величин. •
|
|
| Контроль надежности по косвенным признакам. Первичный и вторичный анализ отказов.
|
|
| Контроль надежности по методу однократной выборки при известном законе распределения.
|
|
| Контроль надежности по методу однократной выборки при неизвестном законе распределения.
|
|
| Контроль надежности по шумовым характеристикам.
|
|
| Контрольные испытания на надежность. Статистические методы контроля надежности.
|
|
| Контрольные испытания на надежность. Схемы испытаний.
|
|
| Надежность невосстанавливаемых резервированных систем.
|
|
| Надежность. Три этапа в развитии
|
|
| Непараметрический метод контроля. Испытания основанные на числе допустимых отказов
|
|
| Неразрушающие методы контроля и их классификация.
|
|
| Общее постоянное резервирование с дробной кратностью.
|
|
| Общее постоянное резервирование с целой кратностью.
|
|
| Общее резервирование замещением с целой кратностью.
|
|
| Общие и частные свойства композиции распределений случайных величин
|
|
| Общие принципы обеспечения надежности сложных технических систем
|
|
| Окончательный расчет надежности
|
|
| Оперативная характеристика плана контроля надежности. Риск поставщика
|
|
| Определение вида закона распределения по результатам испытаний.
|
|
| Определительные испытания. Расчет объема выборки.
|
|
| Определительные испытания. Статистическая оценка параметров распределения.
|
|
| Ориентировочный расчет надежности
|
|
| Основные задачи теории надёжности
|
|
| Основные положения выборочных испытаний. Методы формирования выборок.
|
|
| Отказ. Классификация отказов.
|
|
| Оценка параметров экспоненциального распределения. Интервальная оценка
|
|
| Оценка параметров экспоненциального распределения. Точечная оценка
|
|
| Планирование определительных испытаний. Планы определительных испытаний.
|
|
| Показатели надежности невосстанавливаемых изделий. Вероятностные
|
|
| Показатели надежности невосстанавливаемых изделий. Показатели долговечности
|
|
| Показатели надежности невосстанавливаемых изделий. Статистические
|
|
| Последовательный метод контроля надежности
|
|
| Прикидочный расчет надежности
|
|
| Раздельное постоянное резервирование с целой кратностью.
|
|
| Раздельное резервирование замещением с целой кратностью.
|
|
| Расчет надежности по постепенным отказам. Оно же 60.
|
|
| Расчет надежности по постепенным отказам. Граничные характеристики.
|
|
| Расчет структурной надежности. Функционально-надежностная схема
|
|
| Резервирование с двумя видами отказов. Параллельно-последовательные
|
|
| Свойства надежности, количественные показатели надежности.
|
|
| Скользящее резервирование.
|
|
| Случайные величины и их характеристики.
|
|
| Сравнительная оценка способов резервирования.
|
|
| Стандартизация в области надежности
|
|
| Уравнение Вольтерра.
|
|
| Ускоренные испытания. Коэффициент ускорения.
|
|
| Физическое направление теории надежности.
|
|
| Функциональная и динамическая устойчивость и параметрическая надежность.
|
|
| Электропараметрические методы диагностики. Контроль по ВАХ.
|
|
| Электропараметрические методы диагностики. Метод от-характеристик.
|

 . (26)
. (26) , например, от температуры
, например, от температуры  или времени эксплуатации
или времени эксплуатации  ;
; ;
; , (27)
, (27) совпадает с номинальным значением
совпадает с номинальным значением  .
.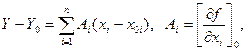 (28)
(28) (29)
(29) – коэффициент корреляции случайных величин x i и х j.
– коэффициент корреляции случайных величин x i и х j. (30)
(30)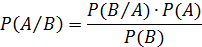
 — вероятность
— вероятность  гипотезы A при наступлении события B (апостериорная вероятность), — вероятность наступления события B при истинности гипотезы A, P (B) — вероятность наступления события B.
гипотезы A при наступлении события B (апостериорная вероятность), — вероятность наступления события B при истинности гипотезы A, P (B) — вероятность наступления события B. , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле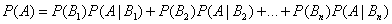 .
. . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий  ,
, .
.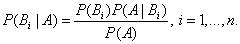
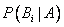 называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как 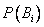 - априорными вероятностями.
- априорными вероятностями.


